题目内容
若椭圆和双曲线具有相同的焦点F1,F2,离心率分别为e1,e2,P是两曲线的一个公共点,且满足PF1⊥PF2,则
+
的值为( )
| 1 | ||
|
| 1 | ||
|
| A.4 | B.2 | C.1 | D.
|
由题意设焦距为2c,椭圆的长轴长2a,双曲线的实轴长为2m,不妨令P在双曲线的右支上
由双曲线的定义|PF1|-|PF2|=2m①,由椭圆的定义|PF1|+|PF2|=2a②
又PF1⊥PF2,∴∠F1PF2=90°,∴|PF1|2+|PF2|2=4c2 ③
①2+②2得|PF1|2+|PF2|2=2a2+2m2④
由③④得a2+m2=2c2,即
+
=1,
∴
+
=2
故选B.
由双曲线的定义|PF1|-|PF2|=2m①,由椭圆的定义|PF1|+|PF2|=2a②
又PF1⊥PF2,∴∠F1PF2=90°,∴|PF1|2+|PF2|2=4c2 ③
①2+②2得|PF1|2+|PF2|2=2a2+2m2④
由③④得a2+m2=2c2,即
| 1 | ||
|
| 1 | ||
|
∴
| 1 | ||
|
| 1 | ||
|
故选B.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
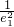 +
+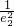 的值为
的值为
 +
+ 的值为( )
的值为( )
 +
+ 的值为( )
的值为( )