题目内容
在△ABC中,已知 ,该三角形的最长边为1,
,该三角形的最长边为1,(Ⅰ)求角C;
(Ⅱ)求△ABC的面积S.
【答案】分析:(Ⅰ)根据两角和的正切函数的公式求出tan(A+B)的值,根据三角形的内角和定理得到A+B的度数即可得到C的度数;
(Ⅱ)因为三角形为钝角三角形,∠C为钝角,所以c=1,然后利用先切互化公式求出sinB和sinA,再根据正弦定理求出b,利用正弦定理求出三角形的面积即可.
解答:解:(Ⅰ)由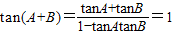 ,
,
而在△ABC中,0<A+B<π,
所以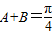 ,则
,则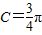 ;
;
(Ⅱ)在△ABC中,
∵∠C是钝角,
∴边c最长,从而c=1
由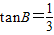 ,得
,得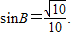
由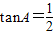 ,得
,得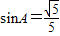
由正弦定理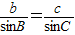 ,得
,得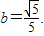
∴△ABC的面积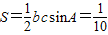 .
.
点评:考查学生会根据三角函数的值求对应的角,灵活运用先切互化的公式解决问题,以及会用正弦定理求三角形的面积.
(Ⅱ)因为三角形为钝角三角形,∠C为钝角,所以c=1,然后利用先切互化公式求出sinB和sinA,再根据正弦定理求出b,利用正弦定理求出三角形的面积即可.
解答:解:(Ⅰ)由
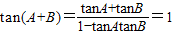 ,
,而在△ABC中,0<A+B<π,
所以
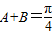 ,则
,则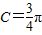 ;
;(Ⅱ)在△ABC中,
∵∠C是钝角,
∴边c最长,从而c=1
由
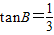 ,得
,得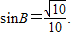
由
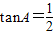 ,得
,得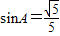
由正弦定理
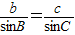 ,得
,得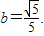
∴△ABC的面积
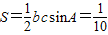 .
.点评:考查学生会根据三角函数的值求对应的角,灵活运用先切互化的公式解决问题,以及会用正弦定理求三角形的面积.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目