题目内容
(本小题满分13分)
在锐角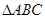 中,已知内角
中,已知内角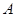 .
.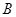 .
.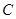 所对的边分别为
所对的边分别为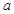 .
.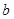 .
.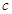 ,向量
,向量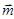
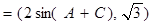 ,
,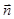
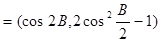 ,且向量
,且向量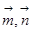 共线.
共线.
(1)求角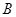 的大小;
的大小;
(2)如果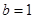 ,求
,求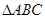 的面积
的面积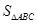 的最大值.
的最大值.
在锐角
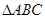 中,已知内角
中,已知内角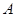 .
.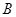 .
.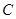 所对的边分别为
所对的边分别为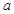 .
.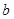 .
.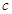 ,向量
,向量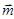
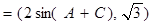 ,
,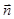
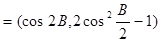 ,且向量
,且向量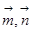 共线.
共线.(1)求角
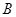 的大小;
的大小;(2)如果
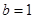 ,求
,求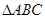 的面积
的面积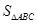 的最大值.
的最大值.解:(1)由向量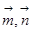 共线有:
共线有: 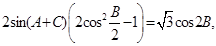
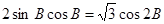 …………………………………………2分
…………………………………………2分
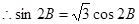 即
即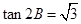 ,……………………… 4分
,……………………… 4分
又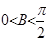 ,所以
,所以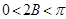 ,则
,则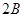 =
=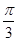 ,即
,即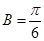 …………………6分
…………………6分
(2)由余弦定理得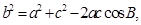 即
即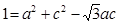 ……7分
……7分
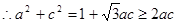 ,当且仅当
,当且仅当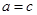 时等号成立……………9分
时等号成立……………9分
所以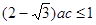 , 得
, 得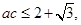
所以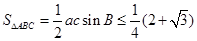 .……………………………… 12分
.……………………………… 12分
所以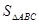 的最大值为
的最大值为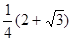 ……………………………… 13分
……………………………… 13分
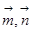 共线有:
共线有: 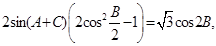
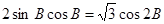 …………………………………………2分
…………………………………………2分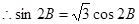 即
即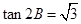 ,……………………… 4分
,……………………… 4分又
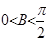 ,所以
,所以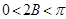 ,则
,则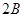 =
=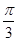 ,即
,即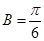 …………………6分
…………………6分(2)由余弦定理得
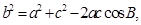 即
即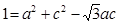 ……7分
……7分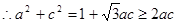 ,当且仅当
,当且仅当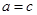 时等号成立……………9分
时等号成立……………9分所以
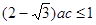 , 得
, 得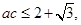
所以
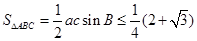 .……………………………… 12分
.……………………………… 12分所以
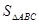 的最大值为
的最大值为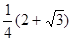 ……………………………… 13分
……………………………… 13分试题分析:(1)根据共线向量的坐标满足的关系得到一个关系式,利用二倍角的正弦函数公式及同角三角函数间的基本关系化简,即可求出tan2B的值,然后由锐角B的范围求出2B的范围,利用特殊角的三角函数值即可求出B的度数;
(2)由b,cosB的值,利用余弦定理及基本不等式即可求出ac的最大值,根据三角形的面积公式进而得到三角形ABC面积的最大值。
解:(1)由向量
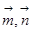 共线有:
共线有: 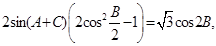
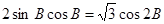 …………………………………………2分
…………………………………………2分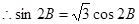 即
即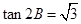 ,……………………… 4分
,……………………… 4分又
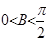 ,所以
,所以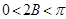 ,则
,则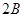 =
=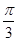 ,即
,即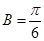 …………………6分
…………………6分(2)由余弦定理得
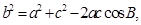 即
即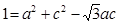 ……7分
……7分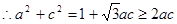 ,当且仅当
,当且仅当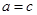 时等号成立……………9分
时等号成立……………9分所以
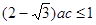 , 得
, 得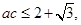
所以
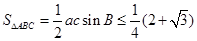 .……………………………… 12分
.……………………………… 12分所以
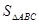 的最大值为
的最大值为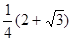 ……………………………… 13分
……………………………… 13分点评:解决该试题的难点是运用均值不等式得到ac的最大值。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的值为 ( )
的值为 ( )

 .
. ; (Ⅱ)已知
; (Ⅱ)已知 ,求
,求 ,则△ABC的形状为
,则△ABC的形状为 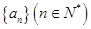 满足:
满足: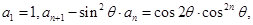 其中
其中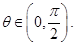
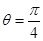 时,求
时,求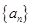 的通项公式;
的通项公式;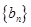 中,
中,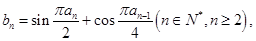 且
且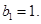 求证:对于
求证:对于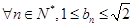 恒成立;
恒成立;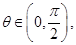 设
设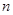 项和为
项和为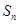 ,试比较
,试比较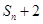 与
与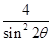 的大小.
的大小. 中,
中, ,三角形面积为
,三角形面积为 ,则
,则 的值为 .
的值为 . 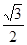 的是 ( )
的是 ( )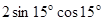
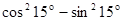
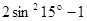
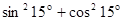
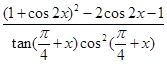
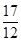 π)的值;
π)的值;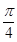 )∪(
)∪(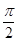 ]时,求g(x)=
]时,求g(x)=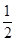 f(x)+sin2x的最大值和最小值.
f(x)+sin2x的最大值和最小值.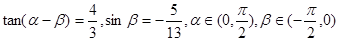 ,则
,则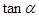 =______.
=______.