题目内容
已知直线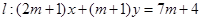 ,圆
,圆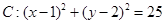
(1)判断直线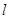 和圆
和圆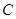 的位置关系;
的位置关系;
(2)若直线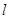 和圆
和圆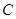 相交,求相交弦长最小时
相交,求相交弦长最小时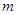 的值.
的值.
【答案】
(1)直线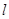 和圆
和圆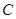 相交;(2)
相交;(2)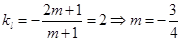 。
。
【解析】本试题主要是考查了直线与圆的位置关系综合运用。
(1)因为利用圆心到直线的距离与圆的半径的关系,来确定结论。
(2)假设直线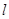 和圆
和圆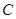 相交于点
相交于点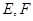 ,由相交弦长公式
,由相交弦长公式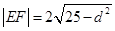 ,其中
,其中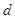 为圆心
为圆心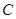 到直线
到直线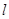 的距离,根据d的最大时的情况得到结论。
的距离,根据d的最大时的情况得到结论。
解:(1)直线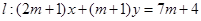 ,
,
即为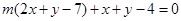 ,
,
则直线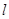 经过直线
经过直线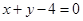 与
与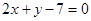 的交点
的交点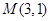
而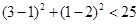 ,所以点
,所以点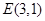 在圆
在圆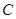 的内部,所以直线
的内部,所以直线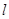 和圆
和圆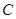 相交;
相交;
(2)假设直线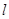 和圆
和圆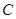 相交于点
相交于点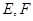 ,由相交弦长公式
,由相交弦长公式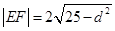 ,其中
,其中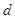 为圆心
为圆心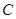 到直线
到直线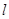 的距离,有公式可知,
的距离,有公式可知,
当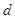 最大时,相交弦长最小,而由(1)知,
最大时,相交弦长最小,而由(1)知,
直线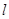 过定点
过定点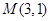 ,所以
,所以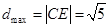 ,即
,即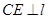 ,又
,又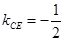 ,所以,
,所以,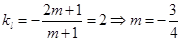

练习册系列答案
相关题目