题目内容
(本题满分12分)数列 满足
满足 ,
, .
.
(1)设 ,是否存在实数
,是否存在实数 ,使得
,使得 是等比数列;
是等比数列;
(2)是否存在不小于2的正整数 ,使得
,使得 成立?若存在,求出
成立?若存在,求出 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.
解:(1)如果存在实数 满足条件,则由已知得
满足条件,则由已知得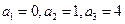 ,
,
所以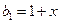 ,
, ,
, 。
。
又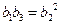 ,所以
,所以 ,解得
,解得 或
或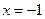 。….2分
。….2分
经检验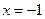 不合题意,舍去;
不合题意,舍去; 适合题意,可得
适合题意,可得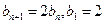 。
。
此时数列 是等比数列,所以存在实数
是等比数列,所以存在实数 使得数列
使得数列 是等比数列。…..4分
是等比数列。…..4分
(2)由上面可得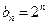 ,所以
,所以 ,所以
,所以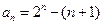 。….6分
。….6分
先证明,当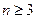 时,
时, ,用数学归纳法
,用数学归纳法
①当 时,
时, ,
, ,所以
,所以 成立;
成立;
②假设当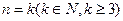 时,
时, 成立,即
成立,即 ,
,
则当 时,
时,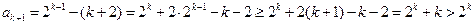
即当 时,
时, 也成立.
也成立.
由①②可得,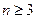 时,
时, 恒成立
恒成立
所以 …11分
…11分
即不存在适合题设条件的正整数 。
。
解析

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案(本题满分12分)
某校为了探索一种新的教学模式,进行了一项课题实验,乙班为实验班,甲班为对比班,甲乙两班的人数均为50人,一年后对两班进行测试,成绩如下表(总分:150分):
甲班
|
成绩 |
|
|
|
|
|
|
频数 |
4 |
20 |
15 |
10 |
1 |
乙班
|
成绩 |
|
|
|
|
|
|
频数 |
1 |
11 |
23 |
13 |
2 |
(1)现从甲班成绩位于 内的试卷中抽取9份进行试卷分析,请问用什么抽样方法更合理,并写出最后的抽样结果;
内的试卷中抽取9份进行试卷分析,请问用什么抽样方法更合理,并写出最后的抽样结果;
(2)根据所给数据可估计在这次测试中,甲班的平均分是101.8,请你估计乙班的平均分,并计算两班平均分相差几分;
(3)完成下面2×2列联表,你认为在犯错误的概率不超过0.025的前提下, “这两个班在这次测试中成绩的差异与实施课题实验有关”吗?并说明理由。
|
|
成绩小于100分 |
成绩不小于100分 |
合计 |
|
甲班 |
|
26 |
50 |
|
乙班 |
12 |
|
50 |
|
合计 |
36 |
64 |
100 |
附:
|
|
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
|
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
18.
(本题满分12分)汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆);
|
|
轿车A |
轿车B |
轿车C |
|
舒适型 |
100 |
150 |
z |
|
标准型 |
300 |
450 |
600 |
按类型用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(Ⅰ)求z的值;
(Ⅱ)用分层抽样的方法在C类轿车中抽取一个容量为5的样本,将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(Ⅲ)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2.把这8辆轿车的得分看成一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率
 ,如下表:
,如下表: 、
、 、
、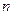 为递减的等差数列,且第一组与第八组的频数相同,求出
为递减的等差数列,且第一组与第八组的频数相同,求出 、
、 ,求事件“
,求事件“ ”的概率.
”的概率.










 ,记数列
,记数列 为
为 ,求
,求