题目内容
a，b，c∈R+，设S=
+
+
+
，则下列判断中正确的是（ ）
| a |
| a+b+c |
| b |
| b+c+d |
| c |
| c+d+a |
| d |
| d+a+b |
| A、0＜S＜1 |
| B、1＜S＜2 |
| C、2＜S＜3 |
| D、3＜S＜4 |
分析：要判断所给的式子的范围，观察式子的特点，分母是一个利用四个字母中的三个做分母的题目，采用放缩法把三个字母的和变化为这四个字母的和，在把所得的结果相加，得到结论，同时以两个为一组，进行放缩，得到式子小于2，得到结果．
解答：解：
+
+
+
＞
+
+
+
=
=1
即S＞1，
＜
，
＜
，
＜
，
＜
得
+
＜
+
=1，
+
＜
+
=1
即
+
+
+
＜2，
得S＜2，所以1＜S＜2．
故选B．
| a |
| a+b+c |
| b |
| b+c+d |
| c |
| c+d+a |
| d |
| d+a+b |
| a |
| a+b+c+d |
| b |
| b+c+d+a |
| c |
| c+d+a+b |
| d |
| d+a+b+c |
=
| a+b+c+d |
| a+b+c+d |
即S＞1，
| a |
| a+b+c |
| a |
| a+c |
| c |
| c+d+a |
| c |
| a+c |
| b |
| b+c+d |
| b |
| b+d |
| d |
| d+a+b |
| d |
| d+b |
得
| a |
| a+b+c |
| c |
| c+d+a |
| c |
| a+c |
| a |
| a+c |
| b |
| b+c+d |
| d |
| d+a+b |
| d |
| d+b |
| b |
| b+d |
即
| a |
| a+b+c |
| b |
| b+c+d |
| c |
| c+d+a |
| d |
| d+a+b |
得S＜2，所以1＜S＜2．
故选B．
点评：本题考查放缩法求解一个式子的取值范围，是一个典型的放缩法，两端都可以变化，可大可小，这种问题经常出现在高考卷中的大型综合题目中．
练习册系列答案
相关题目
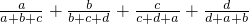，则下列判断中正确的是
，则下列判断中正确的是（ ）