题目内容
已知函数f(x)=-x3+ax2+bx+c在(-∞,0)上是减函数,在(0,1)上是增函数,函数f(x)在R上有三个零点,且1是其中一个零点.
(1)求b的值 (2)求f(2)的取值范围
(1) b=0(2) 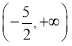
【解析】
试题分析:(1)由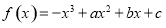 ,得:
,得: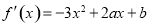 ,根据题设可判定
,根据题设可判定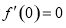 ,从而解得
,从而解得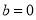 ;
;
(2)由(1)知: ,由
,由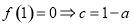 ,所以,
,所以,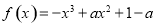
因为函数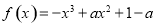 在(-∞,0)上是减函数,在(0,1)上是增函数,函数f(x)在R上有三个零点,且1是其中一个零点,所以
在(-∞,0)上是减函数,在(0,1)上是增函数,函数f(x)在R上有三个零点,且1是其中一个零点,所以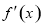 的零点
的零点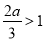 ,得到函数解析式所剩唯一参数
,得到函数解析式所剩唯一参数 的取值范围,进而可求
的取值范围,进而可求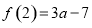 的取值范围.
的取值范围.
试题解析:
(1)∵f(x)=-x3+ax2+bx+c,
∴f ′(x)=-3x2+2ax+b. 3分
∵f(x)在(-∞,0)上是减函数,在(0,1)上是增函数,
∴当x=0时,f(x)取到极小值,即f ′(0)=0,
∴b=0. 6分
(2)由(1)知,f(x)=-x3+ax2+c,
∵1是函数f(x)的一个零点,即f(1)=0,∴c=1-a.
∵f′(x)=-3x2+2ax=0的两个根分别为x1=0,x2=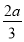 . 9分
. 9分
又∵f(x)在(-∞,0)上是减函数,在(0,1)上是增函数,且函数f(x)在R上有三个零点,
∴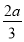 应是f(x)的一个极大值点,因此应有x2=
应是f(x)的一个极大值点,因此应有x2=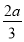 >1,即a>
>1,即a> .
.
∴f(2)=-8+4a+(1-a)=3a-7>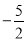 .
.
故f(2)的取值范围为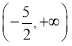 . 13分
. 13分
考点:导数在研究函数性质中的应用.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目


































