题目内容
已知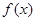 是定义在
是定义在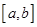 上的函数,其图象是一条连续的曲线,且满足下列条件:①
上的函数,其图象是一条连续的曲线,且满足下列条件:①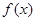 的值域为M,且MÍ
的值域为M,且MÍ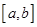 ;②对任意不相等的
;②对任意不相等的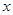 ,
,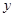 ∈
∈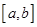 , 都有|
, 都有|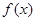 -
-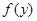 |<|
|<|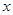 -
-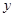 |.
|.
那么,关于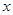 的方程
的方程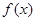 =
=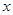 在区间
在区间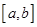 上根的情况是 ( )
上根的情况是 ( )
A.没有实数根 B.有且仅有一个实数根
C.恰有两个不等的实数根 D.有无数个不同的实数根
【答案】
B
【解析】设g(x)=f(x)-x.g(a)=f(a)-a≥0,g(b)=f(b)-b≤0,
所以g(x)=0在[a,b]有实数根,若有两个不同的实数根x,y,
则f(x)=x,f(y)=y,得f(x)-f(y)=x-y,这与已知条件|f(x)-f(y)|<|x-y|相矛盾.
所以关于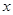 的方程
的方程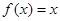 在区间
在区间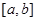 上有且仅有一个实数根
上有且仅有一个实数根

练习册系列答案
相关题目
 是定义在
是定义在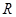 上的函数,
上的函数,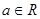 ,那么“对任意的
,那么“对任意的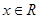 ,
,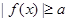 恒成立”的充要条件是( )
恒成立”的充要条件是( )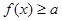 或
或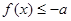 恒成立
恒成立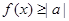 或
或 恒成立
恒成立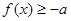 恒成立
恒成立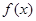 是定义在
是定义在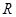 上的函数,且满足
上的函数,且满足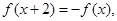 当
当 时,
时, ,则
,则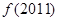 等于 A.
等于 A.
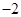 B.2 C.
B.2 C. 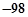 D.
98
D.
98 是定义在
是定义在 上的函数,对任意
上的函数,对任意 都有
都有 ,若函数
,若函数 的图象关于直线
的图象关于直线 对称,且
对称,且 ,则
,则 等于
等于