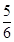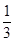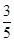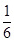题目内容
已知各项均不相等的等差数列{an}的前四项和S4=14,且a1,a3,a7成等比数列.
(1)求数列{an}的通项公式;
(2)设Tn为数列{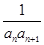 }的前n项和,若Tn≤λan+1对?n∈N*恒成立,求实数λ的最小值.
}的前n项和,若Tn≤λan+1对?n∈N*恒成立,求实数λ的最小值.
(1)求数列{an}的通项公式;
(2)设Tn为数列{
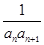 }的前n项和,若Tn≤λan+1对?n∈N*恒成立,求实数λ的最小值.
}的前n项和,若Tn≤λan+1对?n∈N*恒成立,求实数λ的最小值.解:(1)设公差为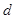 。由已知得
。由已知得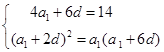 ………………………3分
………………………3分
解得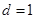 或
或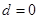 (舍去) 所以
(舍去) 所以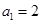 ,故
,故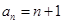 ………………………………6分
………………………………6分
(2)因为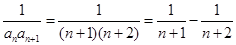
所以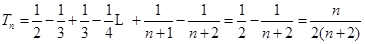 ………………………9分
………………………9分
因为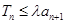 对
对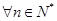 恒成立。即,
恒成立。即,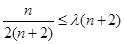 ,对
,对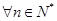 恒成立。
恒成立。
又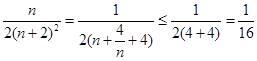
所以实数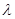 的最小值为
的最小值为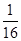 ………………………………………………………………12分
………………………………………………………………12分
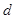 。由已知得
。由已知得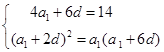 ………………………3分
………………………3分解得
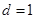 或
或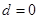 (舍去) 所以
(舍去) 所以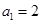 ,故
,故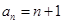 ………………………………6分
………………………………6分(2)因为
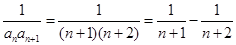
所以
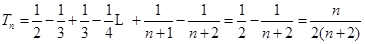 ………………………9分
………………………9分因为
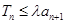 对
对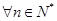 恒成立。即,
恒成立。即,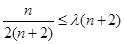 ,对
,对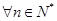 恒成立。
恒成立。又
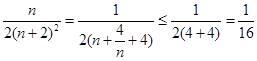
所以实数
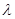 的最小值为
的最小值为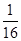 ………………………………………………………………12分
………………………………………………………………12分略

练习册系列答案
相关题目
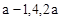 ,记前n项和为Sn
,记前n项和为Sn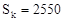 ,求a和k的值;
,求a和k的值;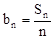 ,求
,求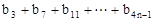 的值
的值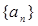 中,已知
中,已知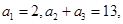 则
则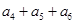 等于( )
等于( )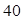
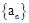 中,
中,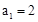 ,
,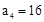 。
。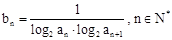 ,求数列
,求数列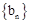 的前n项和
的前n项和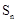 。
。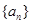 中,
中,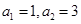 ,数列
,数列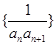 的前
的前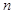 项和为
项和为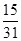 ,则
,则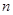 的值为( )
的值为( )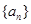 的前n项和为
的前n项和为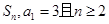 ,
,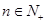 ,满足
,满足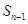 是
是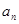 与-3的等差中项。
与-3的等差中项。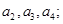
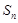 是等差数列
是等差数列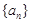 的前
的前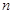 项和,
项和,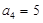 ,
,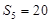 ,则
,则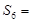 _______.
_______.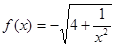 ,数列
,数列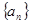 的前
的前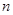 项和为
项和为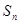 ,点
,点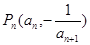 在曲线
在曲线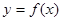 上
上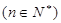 ,
,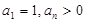
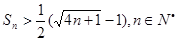 ,
,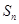 是等差数列{
是等差数列{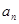 }的前n项和,S5=3(a2+a8),则
}的前n项和,S5=3(a2+a8),则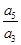 的值为
的值为