题目内容
已知两点 及
及 ,点
,点 在以
在以 、
、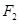 为焦点的椭圆
为焦点的椭圆 上,且
上,且 、
、 、
、 构成等差数列.
构成等差数列.

(1)求椭圆 的方程;
的方程;
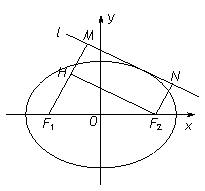
(2)如图,动直线 与椭圆
与椭圆 有且仅有一个公共点,点
有且仅有一个公共点,点 是直线上的两点,且
是直线上的两点,且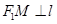 ,
, . 求四边形
. 求四边形 面积
面积 的最大值.
的最大值.
【答案】
(1) (2)
(2)
【解析】
试题分析:解:(1)依题意,设椭圆 的方程为
的方程为 .
.
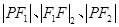 构成等差数列,
构成等差数列,
 ,
,  .又
.又 ,
, .
.
 椭圆
椭圆 的方程为
的方程为 .
.
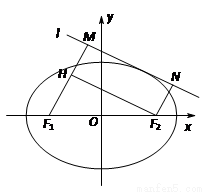
(2) 将直线的方程 代入椭圆
代入椭圆 的方程
的方程 中,得
中,得 .
.
由直线与椭圆 仅有一个公共点知,
仅有一个公共点知, ,
,
化简得: .
.
设 ,
, ,
,
(法一)当 时,设直线的倾斜角为
时,设直线的倾斜角为 ,
,
则 ,
,
 ,
,

 ,
11分
,
11分

 ,
, 当
当 时,
时, ,
,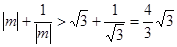 ,
, .
.
当 时,四边形
时,四边形 是矩形,
是矩形, .
.
所以四边形 面积
面积 的最大值为
的最大值为 .
.
(法二)
 ,
,
 .
.

 .
.
四边形 的面积
的面积
 ,
,

 .
.
当且仅当 时,
时, ,故
,故 .
.
所以四边形 的面积
的面积 的最大值为
的最大值为 .
.
考点:直线与椭圆的位置关系
点评:主要是考查了直线与椭圆的位置关系的运用,属于中档题。

练习册系列答案
相关题目
 及
及 ,点
,点 在以
在以 、
、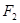 为焦点的椭圆
为焦点的椭圆 上,且
上,且 、
、 、
、 构成等差数列.
构成等差数列. 与椭圆
与椭圆 是直线
是直线 上的两点,且
上的两点,且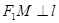 ,
, .
求四边形
.
求四边形 面积
面积 的最大值.
的最大值. 及
及 ,点
,点 在以
在以 、
、 为焦点的椭圆
为焦点的椭圆 上,且
上,且 、
、 、
、 构成等差数列.
构成等差数列. 与椭圆
与椭圆 是直线
是直线 上的两点,且
上的两点,且 ,
, .
求四边形
.
求四边形 面积
面积 的最大值.
的最大值.
 及
及 ,点
,点 在以
在以 、
、 为焦点的椭圆
为焦点的椭圆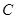 上,且
上,且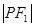 、
、 、
、 构成等差数列.
构成等差数列.
 与椭圆
与椭圆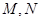 是直线
是直线 上的两点,且
上的两点,且 ,
,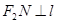 . 求四边形
. 求四边形 面积
面积 的最大值.
的最大值.