题目内容
 (2013•房山区一模)在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,ABCD为直角梯形,BC∥AD,∠ADC=90°,BC=CD=
(2013•房山区一模)在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,ABCD为直角梯形,BC∥AD,∠ADC=90°,BC=CD=| 1 | 2 |
(Ⅰ)求证:PA∥平面BEF;
(Ⅱ)若PC与AB所成角为45°,求PE的长;
(Ⅲ)在(Ⅱ)的条件下,求二面角F-BE-A的余弦值.
分析:(Ⅰ)因为F为PC的中点,可联想连结AC,交BE于一点O,即可证明O点为AC的中点,利用三角形中位线知识证得线线平行,从而得到线面平行;
(Ⅱ)以E点为坐标原点,建立空间直角坐标系,利用两条异面直线所成角为45°,结合给出的线段的长度,即可求出PE的长度;
(Ⅲ)求出两个平面FBE与BEA的法向量,利用两个平面法向量所成的角求二面角的余弦值.
(Ⅱ)以E点为坐标原点,建立空间直角坐标系,利用两条异面直线所成角为45°,结合给出的线段的长度,即可求出PE的长度;
(Ⅲ)求出两个平面FBE与BEA的法向量,利用两个平面法向量所成的角求二面角的余弦值.
解答:(Ⅰ)证明:连接AC交BE于O,并连接EC,FO,
∵BC∥AD,BC=
AD,E为AD中点,∴AE∥BC,且AE=BC.
∴四边形ABCE为平行四边形,则O为AC中点.
又F为AD中点,∴OF∥PA.∵OF?平面BEF,PA?平面BEF.∴PA∥平面BEF.
(Ⅱ)解:∵PA=PD,E为AD中点,∴PE⊥AD.
∵侧面PAD⊥底面ABCD,侧面PAD∩底面ABCD=AD,PE?平面PAD,∴PE⊥平面ABCD.
易知 BCDE为正方形,∴AD⊥BE.
建立如图空间直角坐标系E-xyz,
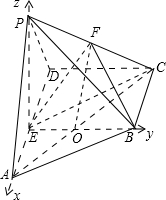
设PE=t(t>0),
则E(0,0,0),A(1,0,0),B(0,1,0),P(0,0,t),C(-1,1,0)
∴
=(-1,1,-t),
=(-1,1,0).
∵PC与AB所成角为45°,
∴|cos<
,
|=|
|=|
|
=cos45°=
,
解得:t=
,∴PE=
.
(Ⅲ)解:∵F为PC的中点,所以F=(-
,
,
),
=(0,1,0),
=(-
,
,
),
设
=(x,y,z)是平面BEF的法向量,
则
取x=2,则z=
,得
=(2,0,
).
=(0,0,
)是平面ABE的法向量.
∴|cos<
,
|=
=
.
由图可知二面角E-AC-B的平面角是钝角,
所以二面角E-AC-B的余弦值为-
.
∵BC∥AD,BC=
| 1 |
| 2 |
∴四边形ABCE为平行四边形,则O为AC中点.
又F为AD中点,∴OF∥PA.∵OF?平面BEF,PA?平面BEF.∴PA∥平面BEF.
(Ⅱ)解:∵PA=PD,E为AD中点,∴PE⊥AD.
∵侧面PAD⊥底面ABCD,侧面PAD∩底面ABCD=AD,PE?平面PAD,∴PE⊥平面ABCD.
易知 BCDE为正方形,∴AD⊥BE.
建立如图空间直角坐标系E-xyz,

设PE=t(t>0),
则E(0,0,0),A(1,0,0),B(0,1,0),P(0,0,t),C(-1,1,0)
∴
| PC |
| AB |
∵PC与AB所成角为45°,
∴|cos<
| PC |
| AB> |
| ||||
|
|
| (-1)×(-1)+1×1+(-t)×0 | ||||
|
=cos45°=
| ||
| 2 |
解得:t=
| 2 |
| 2 |
(Ⅲ)解:∵F为PC的中点,所以F=(-
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| EB |
| EF |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
设
| n |
则
|
取x=2,则z=
| 2 |
| n |
| 2 |
| EP |
| 2 |
∴|cos<
| n |
| EP> |
|
| ||||
|
|
| ||
| 3 |
由图可知二面角E-AC-B的平面角是钝角,
所以二面角E-AC-B的余弦值为-
| ||
| 3 |
点评:本题考查了线面平行的判定,考查了利用空间向量求二面角的余弦值,解答的关键是空间坐标系的正确建立,同时需要注意的是平面法向量所成的角和二面角的关系,此题是中档题.

练习册系列答案
相关题目
 (2013•房山区一模)执行如图所示的程序框图.若输出S=15,则框图中①处可以填入( )
(2013•房山区一模)执行如图所示的程序框图.若输出S=15,则框图中①处可以填入( )