题目内容
函数f(x)=ax+|x-
|-
在(0,1)上有两个不同的零点,则实数a的取值范围是 .
| 1 |
| 2 |
| 1 |
| 2 |
分析:由f(x)=0,得到ax=-|x-
|+
,将方程转化为函数,利用指数函数的图象,结合数形结合的数学思想即可得到结论.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:由f(x)=ax+|x-
|-
=0,
得ax=-|x-
|+
,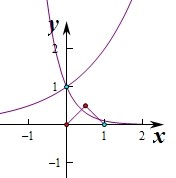
设函数y=ax和y=-|x-
|+
,
作出函数y=-|x-
|+
,在(0,1)上的图象如图:
若a>1,则函数y=ax和y=-|x-
|+
两个图象没有公共点,不成立.
若0<a<1,则函数y=ax单调递减,y=-|x-
|+
在(0,1)上的最大值为
,
要使两个图象有两个不同的公共点,
则当x=
时,满足a
<
,
即a<
,
此时0<a<
,
故答案为:0<a<
.
| 1 |
| 2 |
| 1 |
| 2 |
得ax=-|x-
| 1 |
| 2 |
| 1 |
| 2 |

设函数y=ax和y=-|x-
| 1 |
| 2 |
| 1 |
| 2 |
作出函数y=-|x-
| 1 |
| 2 |
| 1 |
| 2 |
若a>1,则函数y=ax和y=-|x-
| 1 |
| 2 |
| 1 |
| 2 |
若0<a<1,则函数y=ax单调递减,y=-|x-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
要使两个图象有两个不同的公共点,
则当x=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即a<
| 1 |
| 4 |
此时0<a<
| 1 |
| 4 |
故答案为:0<a<
| 1 |
| 4 |
点评:本题主要考查函数零点的应用,将函数零点问题转化为两个函数的图象是解决本题的关键,利用数形结合是基本方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目