题目内容
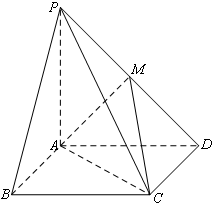如图，四棱锥P-ABCD中，底面ABCD是正方形，PA⊥底面ABCD，M为PD的中点，PA=AB．（I）求直线BC与平面ACM所成角的正弦值；
（II）求平面PAB与平面ACM所成锐二面角的余弦值．
分析：（I）利用VM-ADC=VD-AMC，求出D到平面AMC的距离，从而可得直线AD与平面ACM所成角的正弦值；
（II）过M作ME⊥PA，垂足为E，连接BE，则△ABE为△ACM在平面PAB中的射影，利用面积射影法，可求平面PAB与平面ACM所成锐二面角的余弦值．
（II）过M作ME⊥PA，垂足为E，连接BE，则△ABE为△ACM在平面PAB中的射影，利用面积射影法，可求平面PAB与平面ACM所成锐二面角的余弦值．
解答：解：（I）设PA=AB=2a，D到平面AMC的距离为d，则AM=DM=
a，CM=
a，AD=DC=2a，AC=2
a，
∵AM2+CM2=AC2，∴AM⊥CM
∴S△AMC=
×
a×
a=
a2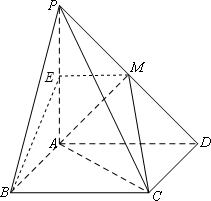
∵S△ADC=2a2
∴由VM-ADC=VD-AMC可得
×2a2×a=
×
a2×d
∴d=
a
∵AD=2a，∴直线AD与平面ACM所成角的正弦值为
∵AD∥BC，∴直线BC与平面ACM所成角的正弦值为
；
（II）过M作ME⊥PA，垂足为E，连接BE，则△ABE为△ACM在平面PAB中的射影
∵AB=2a，AE=a，∴S△ABE=a2
∵S△AMC=
a2
∴平面PAB与平面ACM所成锐二面角的余弦值为
=
．
| 2 |
| 6 |
| 2 |
∵AM2+CM2=AC2，∴AM⊥CM
∴S△AMC=
| 1 |
| 2 |
| 2 |
| 6 |
| 3 |
∵S△ADC=2a2
∴由VM-ADC=VD-AMC可得
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
∴d=
2
| ||
| 3 |
∵AD=2a，∴直线AD与平面ACM所成角的正弦值为
| ||
| 3 |
∵AD∥BC，∴直线BC与平面ACM所成角的正弦值为
| ||
| 3 |
（II）过M作ME⊥PA，垂足为E，连接BE，则△ABE为△ACM在平面PAB中的射影
∵AB=2a，AE=a，∴S△ABE=a2
∵S△AMC=
| 3 |
∴平面PAB与平面ACM所成锐二面角的余弦值为
| S△ABE |
| S△AMC |
| ||
| 3 |
点评：本题考查线面角，考查面面角，解题的关键是求出点到面的距离，确定三角形的面积，属于中档题．
练习册系列答案
相关题目
如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC，
如图，四棱锥P-ABCD中，底面ABCD是直角梯形，AB∥CD，∠DAB=60°，AB=AD=2CD=2，侧面PAD⊥底面ABCD，且△PAD为等腰直角三角形，∠APD=90°，M为AP的中点．
如图，四棱锥P-ABCD的底面ABCD是矩形，AB=2，
如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥底面ABCD，且PA=AB=1，
如图，四棱锥P-ABCD，PA⊥平面ABCD，ABCD是直角梯形，DA⊥AB，CB⊥AB，PA=2AD=BC=2，AB=