题目内容
已知△ABC的三个顶点均在球O的球面上，且AB=AC=1，∠BAC=120°，直线OA与平面ABC所成的角的正弦值为
| ||
| 3 |
分析：欲求球面上B、C两点间的球面距离，作出O到平面ABC的高，判断垂足O′是外心，然后解三角形ABC的外接圆半径和球心角，最后求得P到球面上B、C两点间的球面距离．
解答：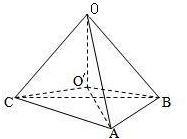
解：在三角形ABC中，AB=AC=1，∠BAC=120°，
∴由余弦定理得BC=
，
由正弦定理得，三角形ABC外接圆的半径O′B=
，如图，
又直线OA与平面ABC所成的角的正弦值为
，
∴
=cos∠OAO′，解得OA=
，
在三角形BCO′中，
∠BO′C=
，球的半径R=
，
则球面上B、C两点间的球面距离为：
×
=
π
故答案为：
π．
解：在三角形ABC中，AB=AC=1，∠BAC=120°，∴由余弦定理得BC=
| 3 |
由正弦定理得，三角形ABC外接圆的半径O′B=
| 3 |
又直线OA与平面ABC所成的角的正弦值为
| ||
| 3 |
∴
| AO′ |
| OA |
| 3 |
在三角形BCO′中，
∠BO′C=
| π |
| 3 |
| 3 |
则球面上B、C两点间的球面距离为：
| π |
| 3 |
| 3 |
| ||
| 3 |
故答案为：
| ||
| 3 |
点评：本题考查棱锥的结构特征，考查正弦定理、余弦定理，球面距离及相关计算，解答关键是明确球面距离的概念，是中档题．
练习册系列答案
口算题天天练系列答案
相关题目
，则球面上B、C两点间的球面距离为 ．