题目内容
若对任意x∈(1,3)的实数,使得不等式2x3+3x2≥6(6x+a)恒成立,求实数a的取值范围.
【答案】分析:假设f(x)=2x3+3x2-36x-6a,x∈(1,3),将问题转化为对任意x∈(1,3)的实数,使得不等式f(x)≥0恒成立.利用导数求出函数的最小值大于等于0即可.
解答:解:设f(x)=2x3+3x2-36x-6a,x∈(1,3)…(4分)
∴f′(x)=6x2+6x-36,
由f′(x)=0得x=2,x=-3.
∵x∈(1,3)
∴当1<x<2时,f′(x)<0,当2<x<3时,f′(x)>0…(8分)
∴f(x)在x=2处取得最小值f(2)=-44-6a≥0
∴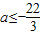 …(10分)
…(10分)
点评:本题考查的重点是恒成立问题,考查利用导数求函数的最值,解题的关键是构造函数求最值.
解答:解:设f(x)=2x3+3x2-36x-6a,x∈(1,3)…(4分)
∴f′(x)=6x2+6x-36,
由f′(x)=0得x=2,x=-3.
∵x∈(1,3)
∴当1<x<2时,f′(x)<0,当2<x<3时,f′(x)>0…(8分)
∴f(x)在x=2处取得最小值f(2)=-44-6a≥0
∴
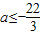 …(10分)
…(10分)点评:本题考查的重点是恒成立问题,考查利用导数求函数的最值,解题的关键是构造函数求最值.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目