题目内容
(理)设a>0,a≠1为常数,函数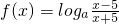
(1)讨论函数f(x)在区间(-∞,-5)内的单调性,并给予证明;
(2)设g(x)=1+loga(x-3),如果方程f(x)=g(x)有实数解,求实数a的取值范围.
解:(1)设t= ,任取x2<x1<-5,则
,任取x2<x1<-5,则
t2-t1= -
-
=
= .
.
∵x1<-5,x2<-5,x2<x1,
∴x1+5<0,x2+5<0,x2-x1<0.
∴ <0,即t2<t1.
<0,即t2<t1.
当a>1时,y=logax是增函数,∴logat2<logat1,即f(x2)<f(x1);
当0<a<1时,y=logax是减函数,∴logat2>logat1,即f(x2)>f(x1).
综上可知,当a>1时,f(x)在区间(-∞,-5)为增函数;
当0<a<1时,f(x)在区间(-∞,-5)为减函数.
(2)g(x)=1+loga(x-3)=logaa(x-3),
方程f(x)=g(x)等价于:
即方程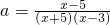 在区间(5,+∞)上有解,
在区间(5,+∞)上有解,
∵ =
=
∴函数F(x)=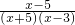 在区间(5,5+2
在区间(5,5+2 )上导数大于零,在区间(5+2
)上导数大于零,在区间(5+2 ,+∞)导数小于零
,+∞)导数小于零
可得F(x)=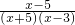 在区间(5,5+2
在区间(5,5+2 )上单调增,在区间(5+2
)上单调增,在区间(5+2 ,+∞)单调减
,+∞)单调减
∴F(x)的最大值为F(5+2 )=
)= ,而F(x)的最小值大于F(5)=0
,而F(x)的最小值大于F(5)=0
要使方程方程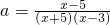 在区间(5,+∞)上有解,必须a∈(0,
在区间(5,+∞)上有解,必须a∈(0, )
)
所以a的取值范围是:(0, )
)
分析:(1)将对数的真数当成一个函数,可以用定义证明它在区间(-∞,-5)内的单调性,再讨论底数a与1的大小关系得到相应的情况下真数的大小关系,即可得函数f(x)在区间(-∞,-5)内的单调性;
(2)化函数g(x)=1+loga(x-3))为g(x)=logaa(x-3),方程f(x)=g(x)即为它们的真数都大于零且相等,采用变量分离的方法,转化为求函数F(x)=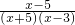 在区间(5,+∞)上的值域,实数a的取值范围就应该属于这个值域.
在区间(5,+∞)上的值域,实数a的取值范围就应该属于这个值域.
点评:本题着重考查了函数单调性的判断与证明、根的存在性及根的个数判断等知识点,在解题时应该注意分类讨论与数形结合等数学思想的应用.
 ,任取x2<x1<-5,则
,任取x2<x1<-5,则t2-t1=
 -
-
=

=
 .
.∵x1<-5,x2<-5,x2<x1,
∴x1+5<0,x2+5<0,x2-x1<0.
∴
 <0,即t2<t1.
<0,即t2<t1.当a>1时,y=logax是增函数,∴logat2<logat1,即f(x2)<f(x1);
当0<a<1时,y=logax是减函数,∴logat2>logat1,即f(x2)>f(x1).
综上可知,当a>1时,f(x)在区间(-∞,-5)为增函数;
当0<a<1时,f(x)在区间(-∞,-5)为减函数.
(2)g(x)=1+loga(x-3)=logaa(x-3),
方程f(x)=g(x)等价于:

即方程
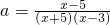 在区间(5,+∞)上有解,
在区间(5,+∞)上有解,∵
 =
=
∴函数F(x)=
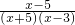 在区间(5,5+2
在区间(5,5+2 )上导数大于零,在区间(5+2
)上导数大于零,在区间(5+2 ,+∞)导数小于零
,+∞)导数小于零可得F(x)=
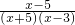 在区间(5,5+2
在区间(5,5+2 )上单调增,在区间(5+2
)上单调增,在区间(5+2 ,+∞)单调减
,+∞)单调减∴F(x)的最大值为F(5+2
 )=
)= ,而F(x)的最小值大于F(5)=0
,而F(x)的最小值大于F(5)=0要使方程方程
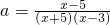 在区间(5,+∞)上有解,必须a∈(0,
在区间(5,+∞)上有解,必须a∈(0, )
)所以a的取值范围是:(0,
 )
)分析:(1)将对数的真数当成一个函数,可以用定义证明它在区间(-∞,-5)内的单调性,再讨论底数a与1的大小关系得到相应的情况下真数的大小关系,即可得函数f(x)在区间(-∞,-5)内的单调性;
(2)化函数g(x)=1+loga(x-3))为g(x)=logaa(x-3),方程f(x)=g(x)即为它们的真数都大于零且相等,采用变量分离的方法,转化为求函数F(x)=
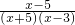 在区间(5,+∞)上的值域,实数a的取值范围就应该属于这个值域.
在区间(5,+∞)上的值域,实数a的取值范围就应该属于这个值域.点评:本题着重考查了函数单调性的判断与证明、根的存在性及根的个数判断等知识点,在解题时应该注意分类讨论与数形结合等数学思想的应用.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
