题目内容
已知圆N:(x+2)2+y2=8和抛物线C: y2= 2x,圆N的切线l与抛物线C交于不同的两点A,B.
(I)当直线l的斜率为1时,求线段AB的长;
(II)设点M和点N关于直线y=x对称,问是否存在直线l,使得 ?若存在,求出直线l的方程;若不存在,请说明理由.
?若存在,求出直线l的方程;若不存在,请说明理由.

(1) .(2)
.(2)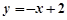 .
.
【解析】(I)直线l的方程为y=x+m,根据直线l与圆相切,求出m值,然后再与抛物线方程联立,根据弦长公式求出AB的值。
(II)由于点M与点N关于直线y=x对称,从而可求出M的坐标,然后利用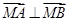 ,把此条件用坐标表示出来,借助韦达定理建立关于k的方程,求出k值,再验证是否满足判别式大于零
,把此条件用坐标表示出来,借助韦达定理建立关于k的方程,求出k值,再验证是否满足判别式大于零
因为圆N: ,所以圆心N为(-2,0),半径
,所以圆心N为(-2,0),半径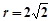 ,
,
………1分
设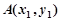 ,
,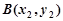 ,
,
(1)当直线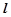 的斜率为1时,设
的斜率为1时,设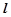 的方程为
的方程为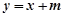 即
即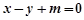 ,因为直线
,因为直线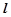 是圆N的切线,所以
是圆N的切线,所以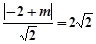 ,解得
,解得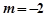 或
或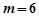 (舍去)
(舍去)
此时直线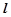 的方程为
的方程为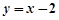 ,
………………3分
,
………………3分
由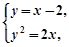 消去
消去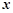 得
得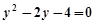 ,所以
,所以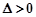 ,
,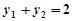 ,
,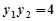 ,
,
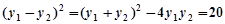
所以弦长 .……………………6分
.……………………6分
(2)①设直线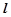 的方程为
的方程为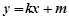 即
即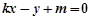 (
(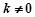 ),
),
因为直线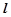 是圆N的切线,所以
是圆N的切线,所以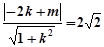 ,
,
得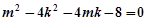 ①………………8分
①………………8分
由 消去
消去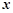 得
得 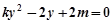 ,
,
所以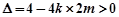 即
即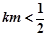 且
且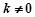 ,
,
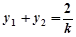 ,
,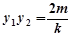 .
.
因为点M和点N关于直线 对称,所以点M为
对称,所以点M为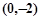
所以 ,
,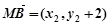 ,
,
因为 ,所以
,所以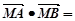
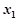
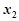 +
+ 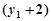
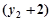
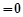 ,……9分
,……9分
将A,B在直线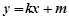 上代入化简得,
上代入化简得,
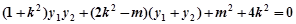 .
.
代入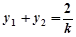 ,
,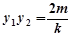 得
得
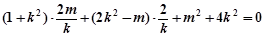
化简得 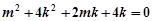 ………②
………②
①+②得 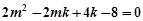
即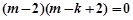 ,解得
,解得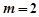 或
或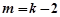
当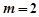 时,代入①解得
时,代入①解得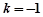 ,满足条件
,满足条件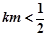 且
且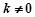 ,
,
此时直线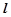 的方程为
的方程为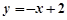 ;
;
当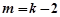 时,代入①整理得
时,代入①整理得 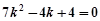 ,无解.………………11分
,无解.………………11分
②
当直线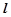 的斜率不存在时,因为直线
的斜率不存在时,因为直线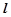 是圆N的切线,所以
是圆N的切线,所以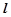 的方程为
的方程为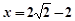 ,则得
,则得 ,
,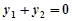 ,
,
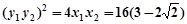 即
即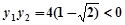
由①得: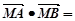
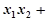
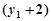
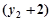
=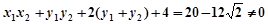
当直线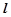 的斜率不存在时
的斜率不存在时 不成立.
不成立.
综上所述,存在满足条件的直线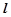 ,其方程为
,其方程为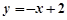 .
.

 快捷英语周周练系列答案
快捷英语周周练系列答案