题目内容
设变量x，y满足约束条件
，则目标函数z=|x+3y|的最大值为（ ）
|
分析：作出不等式组表示的平面区域；作出目标函数对应的直线；结合图象知当直线过A、B时，z最小、最大，从而得出目标函数z=|x+3y|的取值范围，最后得出其最大值．
解答：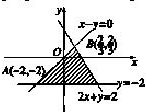
解：画出不等式表示的平面区域
设目标函数为z'=x+3y，作出目标函数对应的直线，
直线过B（
，
）时，直线的纵截距最大，z'最大，最大值为
；
当直线过A（-2，-2）时，直线的纵截距最小，z'最小，最小值为-8；
则目标函数z'=x+3y的取值范围是[-8，
]
∴目标函数z=|x+3y|的取值范围是[0，8]，最大值为8．
故选C．
解：画出不等式表示的平面区域设目标函数为z'=x+3y，作出目标函数对应的直线，
直线过B（
| 2 |
| 3 |
| 2 |
| 3 |
| 8 |
| 3 |
当直线过A（-2，-2）时，直线的纵截距最小，z'最小，最小值为-8；
则目标函数z'=x+3y的取值范围是[-8，
| 8 |
| 3 |
∴目标函数z=|x+3y|的取值范围是[0，8]，最大值为8．
故选C．
点评：本题考查画不等式组表示的平面区域、考查数形结合求函数的最值．
练习册系列答案
相关题目
设变量x，y满足约束条件
，则目标函数u=x2+y2的最大值M与最小值N的比
=（ ）
|
| M |
| N |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|