题目内容
(本大题8分)在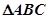 中,
中,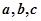 分别是角
分别是角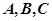 的对边,
的对边,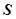 为
为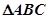 的面积,若
的面积,若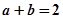 ,且
,且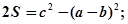
(1).求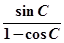 的值; (2).求
的值; (2).求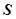 的最大值。
的最大值。
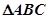 中,
中,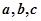 分别是角
分别是角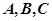 的对边,
的对边,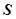 为
为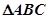 的面积,若
的面积,若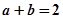 ,且
,且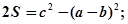
(1).求
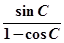 的值; (2).求
的值; (2).求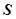 的最大值。
的最大值。(1)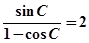
(2)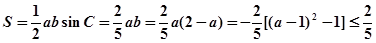
当且仅当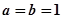 时,面积最大。
时,面积最大。
(1)由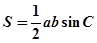 和余弦定理得,
和余弦定理得,
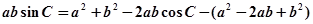 =
=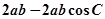
故,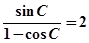 ………………………………………………4分
………………………………………………4分
(2)由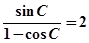 得,
得,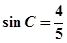
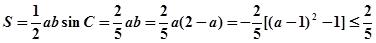 ,
,
当且仅当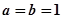 时,面积最大。…………………………4分
时,面积最大。…………………………4分
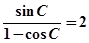
(2)
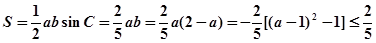
当且仅当
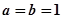 时,面积最大。
时,面积最大。(1)由
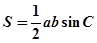 和余弦定理得,
和余弦定理得,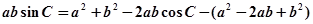 =
=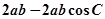
故,
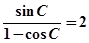 ………………………………………………4分
………………………………………………4分(2)由
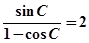 得,
得,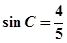
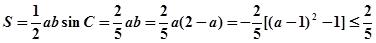 ,
,当且仅当
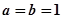 时,面积最大。…………………………4分
时,面积最大。…………………………4分(1)由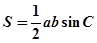 和余弦定理得,
和余弦定理得,
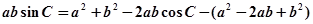 =
=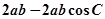 ,
,
进而整理出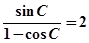 .
.
(2)在(1)的基础上,可求得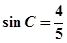 .再根据面积公式
.再根据面积公式 ,注意取得的条件。
,注意取得的条件。
解:(1)由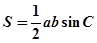 和余弦定理得,
和余弦定理得,
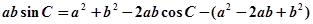 =
=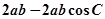
故,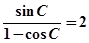 ………………………………………………4分
………………………………………………4分
(2)由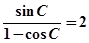 得,
得,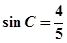
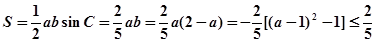 ,
,
当且仅当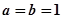 时,面积最大。…………………………4分
时,面积最大。…………………………4分
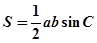 和余弦定理得,
和余弦定理得,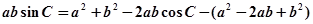 =
=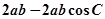 ,
,进而整理出
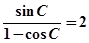 .
.(2)在(1)的基础上,可求得
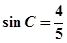 .再根据面积公式
.再根据面积公式 ,注意取得的条件。
,注意取得的条件。解:(1)由
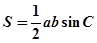 和余弦定理得,
和余弦定理得,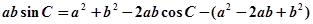 =
=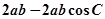
故,
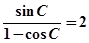 ………………………………………………4分
………………………………………………4分(2)由
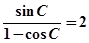 得,
得,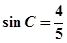
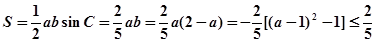 ,
,当且仅当
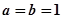 时,面积最大。…………………………4分
时,面积最大。…………………………4分
练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
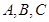 ,下列结论正确的个数是( )
,下列结论正确的个数是( )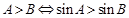 ;②
;②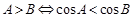 ③
③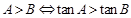
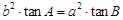 ,那么△ ABC一定是( )
,那么△ ABC一定是( )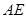 的高度
的高度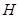 (单位
(单位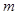 ),如示意图,垂直放置的标杆
),如示意图,垂直放置的标杆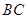 高度
高度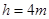 ,仰角
,仰角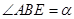 ,
,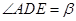 .
.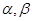 的值,
的值,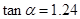 ,
,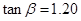 ,请据此算
,请据此算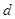 (单位
(单位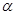 与
与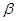 之差较大,可以提高测量精确度,若电视塔实际高度为
之差较大,可以提高测量精确度,若电视塔实际高度为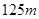 ,问
,问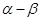 最大?
最大?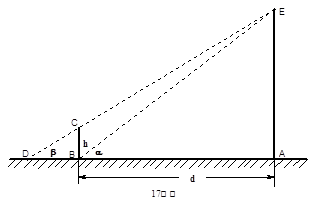
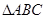 ,内角
,内角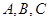 所对的边分别为
所对的边分别为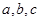 ,且满足下列三个条件:①
,且满足下列三个条件:①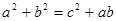 ②
②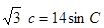 ③
③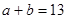
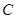 和边长
和边长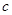 的大小;
的大小; 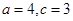 ,则△ABC的面积等于 .
,则△ABC的面积等于 .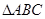 中,∠
中,∠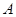 ,∠
,∠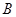 ,∠
,∠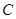 的对边分别是
的对边分别是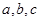 ,若
,若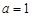 ,
,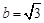 ,
,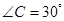 ,则
,则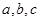 ,若
,若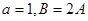 ,则
,则 .
. 中,若
中,若 ,则
,则

