题目内容
已知函数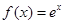 (
(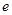 为自然对数的底数),
为自然对数的底数),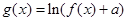 (
(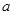 为常数),
为常数),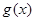 是实数集
是实数集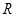 上的奇函数.
上的奇函数.
(1)求证: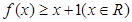 ;
;
(2)讨论关于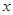 的方程:
的方程: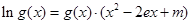
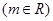 的根的个数;
的根的个数;
(3)设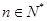 ,证明:
,证明: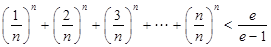 (
(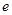 为自然对数的底数).
为自然对数的底数).
【答案】
(1)略
(2)①当 即
即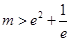 时,方程无根;
时,方程无根;
②当 即
即 时,方程只有一个根.
时,方程只有一个根.
③当 即
即 时,方程有两个根.
时,方程有两个根.
(3)略
【解析】(1)证:令 ,
,
令 时
时
 时,
时,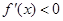 . ∴
. ∴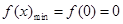
∴ 即
即 .
.
(2)∵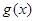 是R上的奇函数
是R上的奇函数
∴ ∴
∴
∴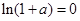 ∴
∴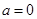 故
故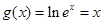 .
.
故讨论方程 在
在 的根的个数.
的根的个数.
即 在
在 的根的个数.
的根的个数.
令 .
.
注意 ,方程根的个数即交点个数.
,方程根的个数即交点个数.
对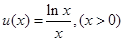 ,
, 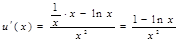 ,
,
令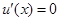 , 得
, 得 ,
,
当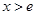 时,
时, ;
当
;
当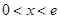 时,
时, .
.
∴ ,
,
当 时,
时,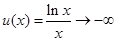 ;
;
当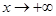 时,
时, , 但此时
, 但此时
 ,此时以
,此时以 轴为渐近线。
轴为渐近线。
①当 即
即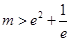 时,方程无根;
时,方程无根;
②当 即
即 时,方程只有一个根.
时,方程只有一个根.
③当 即
即 时,方程有两个根.
时,方程有两个根.
(3)由(1)知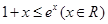 ,
,
令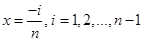 ,
,
∴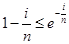 ,于是
,于是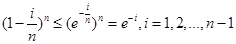 ,
,
∴
 .
.

练习册系列答案
相关题目
 其中
其中 为自然对数的底数,
为自然对数的底数,  .
. ,求函数
,求函数 的最值;
的最值; ,都有
,都有 成立,求
成立,求 的取值范围.
的取值范围. .(
.( 为自然对数的底)
为自然对数的底) 的最小值;
的最小值; 使得
使得 对于任意的正数
对于任意的正数 恒成立?若存在,求出
恒成立?若存在,求出 .e为自然对数的底
.e为自然对数的底 时取得最小值,求
时取得最小值,求 的值;
的值; ,求函数
,求函数 在点P
在点P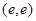 处的切线方程
处的切线方程 其中
其中 为自然对数的底数
为自然对数的底数 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程; 的取值范围;
的取值范围; 时,求函数
时,求函数 的极小值。
的极小值。