题目内容

定义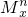 $数学公式$ =x（x+1）（x+2）…（x+n-1），其中x∈R，n∈N^*，例如 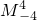$数学公式$ =（-4）（-3）（-2）（-1）=24，则函数f（x）= $数学公式$ 的奇偶性为________．

奇函数
分析：由于f（x）= $\text{[math]}$ =（x-1004）（x-1003）…（x-1）•x•（x+1）…（x+1004），可判断f（-x）=-f（x），从而可得答案．
解答：∵f（x）= $\text{[math]}$ =（x-1004）（x-1003）…（x-1）•x•（x+1）…（x+1004），
∴f（-x）=（-x-1004）（-x-1003）…（-x-1）•（-x）•（-x+1）…（-x+1004）
=（-1）²⁰⁰⁹•（x+1004）（x+1003）…（x+1）•x•（x-1）…（x-1004
=-f（x），
∴f（x）为奇函数．
故答案为：奇函数．
点评：本题考查函数奇偶性的判断，分析得到f（x）=（x-1004）（x-1003）…（x-1）•x•（x+1）…（x+1004）是判断的关键，考查分析与转化的能力，属于中档题．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

名校名师夺冠金卷系列答案

小学英语课时练系列答案

培优新帮手系列答案

天天向上一本好卷系列答案

小学生10分钟应用题系列答案

课堂作业广西教育出版社系列答案

相关题目

已知函数f（x）的图象在[a，b]上连续不断，定义：f₁（x）=min{f（t）|a≤t≤x}（x∈[a，b]），f₂（x）=max{f（t）|a≤t≤x}（x∈[a，b]），其中，min{f（x）|x∈D}表示函数f（x）在D上的最小值，max{f（x）|x∈D}表示函数f（x）在D上的最大值，若存在最小正整数k，使得f₂（x）-f₁（x）≤k（x-a）对任意的x∈[a，b]成立，则称函数f（x）为[a，b]上的“k阶收缩函数”．已知函数f（x）=x²，（x∈[-1，4]）为[-1，4]上的“k阶收缩函数”，则k的取值是

定义M_xⁿ=x（x+1）（x+2）…（x+n-1），其中x∈R，n∈N^*，例如M_-4⁴=（-4）（-3）（-2）（-1）=24，则函数f（x）=M_x-1004²⁰⁰⁹的奇偶性为

已知定义{x∈R|x≠0}的奇函数f（x）在（0，+∞）上为增函数，且f（2）=0，则不等式

＜0的解集为（　　）

A．（-2，0）∪（2，+∞）

B．（-∞，-2）∪（1，2）

C．（-∞，-2）∪（2，+∞）

D．（-2，0）∪（1，2）

（2012•徐汇区一模）对定义在区间D上的函数f（x），若存在闭区间[a，b]⊆D和常数C，使得对任意的x∈[a，b]都有f（x）=C，且对任意的x∉[a，b]都有f（x）＞C恒成立，则称函数f（x）为区间D上的“U型”函数．
（1）求证：函数f（x）=|x-1|+|x-3|是R上的“U型”函数；
（2）设f（x）是（1）中的“U型”函数，若不等式|t-1|+|t-2|≤f（x）对一切的x∈R恒成立，求实数t的取值范围；
（3）若函数g（x）=mx+

是区间[-2，+∞）上的“U型”函数，求实数m和n的值．

已知函数f（x）的图象在[a，b]上连续不断，定义：f₁（x）=min{f（t）|a≤t≤x}（x∈[a，b]），f₂（x）=max{f（t）|a≤t≤x}（x∈[a，b]），其中，min{f（x）|x∈D}表示函数f（x）在D上的最小值，max{f（x）|x∈D}表示函数f（x）在D上的最大值，若存在最小正整数k，使得f₂（x）-f₁（x）≤k（x-a）对任意的x∈[a，b]成立，则称函数f（x）为[a，b]上的“k阶收缩函数”．已知函数f（x）=x²，（x∈[-1，4]）为[-1，4]上的“k阶收缩函数”，则k的取值范围是．