题目内容
一个几何体的三视图如图所示，则其体积等于
A． |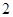
B． |
C． |
D． |
D
解析考点：由三视图求面积、体积．
分析：先由三视图画出几何体的直观图，理清其中的线面关系，再由椎体体积计算公式代入数据计算即可
解：由三视图可知，几何体为一个三棱锥，其直观图如图
，底面三角形为直角三角形，BC=1，AC=2，C=90°
侧棱PC⊥底面ABC，PC=2
∴此几何体的体积为V=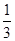
×S△ABC×PC=×
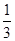×1×2×2=
故选 D
练习册系列答案
相关题目
用一个平面去截一个几何体,得到的截面是圆面,这个几何体不可能是
| A．圆锥 | B．圆柱 | C．球 | D．棱柱 |
一个空间几何体得三视图如图所示，则该几何体的表面积为
第（8）题图
| A．48 | B．32+8 | C．48+8 | D．80 |
一个三棱锥的三视图如右图所示，则其左视图直角三角形的面积是（ ）
A． | B． | C．1 | D． |
个圆台的正视图如图所示，则圆台的体积等于
. 
.
. 
. 
底面半径为2，高为4的圆柱，它的侧面积是（ ）
| A．8p | B．16p | C．20p | D．24p |
D