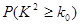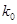题目内容
2013年9月20日是第25个全国爱牙日。某区卫生部门成立了调查小组,调查 “常吃零食与患龋齿的关系”,对该区六年级800名学生进行检查,按患龋齿和不患龋齿分类,得汇总数据:不常吃零食且不患龋齿的学生有60名,常吃零食但不患龋齿的学生有100名,不常吃零食但患龋齿的学生有140名.
|
|
0.010 |
0.005 |
0.001 |
|
|
6.635 |
7.879 |
10.828 |
(1)能否在犯错概率不超过0.001的前提下,认为该区学生的常吃零食与患龋齿有关系?
(2)4名区卫生部门的工作人员随机分成两组,每组2人,一组负责数据收集,另一组负责数据处理.求工作人员甲分到负责收集数据组,工作人员乙分到负责数据处理组的概率.
附: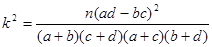
(1)能在犯错率不超过0.001的前提下,为该区学生常吃零食与患龋齿有关系;(2)概率是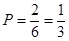 .
.
【解析】
试题分析:本题考查生活中的实际问题、独立性检验问题以及随机事件的概率,考查运用概率知识解决实际问题的能力,考查学生的分析能力和计算能力.第一问,通过分析题意,列出列联表,填出表中所有数据,利用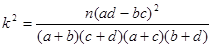 公式计算出数值,与
公式计算出数值,与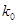 作比较,判断出概率值,从而确定学生常吃零食与患龋齿是否有关系;第二问,先列出4个人收集数据与处理数据的所有情况,再从中挑出符合题意的情况,从而求出概率.
作比较,判断出概率值,从而确定学生常吃零食与患龋齿是否有关系;第二问,先列出4个人收集数据与处理数据的所有情况,再从中挑出符合题意的情况,从而求出概率.
试题解析:(1)由题意可得列联表:
|
|
不常吃零食 |
常吃零食 |
总计 |
|
不患龋齿 |
60 |
100 |
160 |
|
患龋齿 |
140 |
500 |
640 |
|
总计 |
200 |
600 |
800 |
因为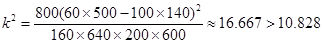 。
。
所以能在犯错率不超过0.001的前提下,为该区学生常吃零食与患龋齿有关系.
(2)设其他工作人员为丙和丁,4人分组的所有情况如下表
|
小组 |
1 |
2 |
3 |
4 |
5 |
6 |
|
收集数据 |
甲乙 |
甲丙 |
甲丁 |
乙丙 |
乙丁 |
丙丁 |
|
处理数据 |
丙丁 |
乙丁 |
乙丙 |
甲丁 |
甲丙 |
甲乙 |
分组的情况总有6中,工作人员甲负责收集数据且工作人员乙负责处理数据占两种,
所以工作人员甲负责收集数据且工作人员乙分到负责处理数据的概率是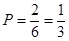 .
.
考点:1.独立性检验;2.列联表;3.随机事件的概率.