题目内容
已知等比数列 的各项均为正数,且
的各项均为正数,且 ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前 项和.
项和.
(1)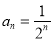 ;(2)数列
;(2)数列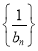 的前
的前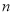 项和为
项和为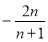 .
.
【解析】
试题分析:(1)先用等比数列的性质化简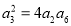 得到公比
得到公比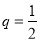 ,然后用首项与公比表示
,然后用首项与公比表示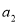 ,可得
,可得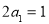 ,从而求出
,从而求出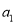 ,最后利用等比数列的通项公式写出通项公式即可;(2)由(1)先求出
,最后利用等比数列的通项公式写出通项公式即可;(2)由(1)先求出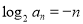 ,从而再利用等差数列的前
,从而再利用等差数列的前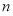 项和公式求出
项和公式求出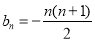 ,从而
,从而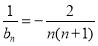 ,最后采用裂项相消法求和即可得到数列
,最后采用裂项相消法求和即可得到数列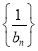 的前
的前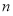 项和.
项和.
试题解析:(1)设等比数列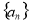 的公比为
的公比为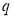 ,由
,由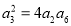 得
得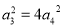 1分
1分
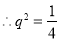 ,由已知
,由已知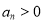 ,
,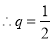 3分
3分
由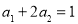 得
得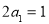 ,
,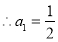 5分
5分
 数列
数列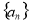 的通项公式为
的通项公式为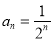 6分
6分
(2)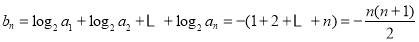 9分
9分
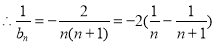 10分
10分
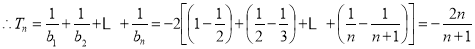
 数列
数列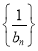 的前
的前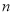 项和为
项和为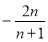 12分.
12分.
考点:1.等比数列的通项公式与性质;2.等差数列的前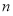 项和公式;3.数列求和的问题.
项和公式;3.数列求和的问题.

练习册系列答案
相关题目