题目内容
Rt△ABC中，∠BAC=90°，作AD⊥BC，D为垂足，BD为AB在BC上的射影，CD为AC在BC上的射影，则有AB2+AC2=BC2，AC2=CD•BC成立．直角四面体P-ABC（即PA⊥PB，PB⊥PC，PC⊥PA）中，O为P在△OCA的面积分别为S1′，S2′，S3′，△ABC的面积记为S．类比直角三角形中的射影结论，在直角四面体P-ABC中可得到正确结论________．（写出一个正确结论即可）
S2=S21+S22+S32
分析：斜边的平方等于两个直角边的平方和，可类比到空间就是斜面面积的平方等于三个直角面的面积的平方和，边对应着面．
解答：由边对应着面，边长对应着面积，
由类比可得S2=S21+S22+S32．
故答案为：S2=S21+S22+S32
点评：本题考查了从平面类比到空间，属于基本类比推理．利用类比推理可以得到结论、证明类比结论时证明过程与其类比对象的证明过程类似或直接转化为类比对象的结论．
分析：斜边的平方等于两个直角边的平方和，可类比到空间就是斜面面积的平方等于三个直角面的面积的平方和，边对应着面．
解答：由边对应着面，边长对应着面积，
由类比可得S2=S21+S22+S32．
故答案为：S2=S21+S22+S32
点评：本题考查了从平面类比到空间，属于基本类比推理．利用类比推理可以得到结论、证明类比结论时证明过程与其类比对象的证明过程类似或直接转化为类比对象的结论．
练习册系列答案
习题精选系列答案
相关题目
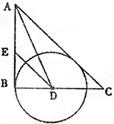16、如图，在Rt△ABC中，∠B=90°，∠A的平分线交BC于D，E为AB上一点，DE=DC，以D为圆心，以DB的长为半径画圆．
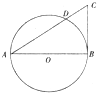（2013•石家庄二模）选修4-1：几何证明选讲
,AB=a,在△ABC内作一系列的正方形，求所有这些正方形的面积和S. 
，点M、N分别在边AB和AC上（点M和点B不重合），将△AMN沿MN翻折到△A′MN，顶点A′恰好落在边BC上（点A′和点B不重合）。
