题目内容
已知函数y=f(x)的图象是自原点出发的一条折线. 当n≤y≤n+1(n=0,1,2,…)时,该图象是斜率为bn的线段(其中正常数b≠1),设数列{xn}由f(xn)=n(n=1,2,…)定义
(Ⅰ)求x1、x2和xn的表达式;
(Ⅱ)计算![]() xn;
xn;
(Ⅲ)求f(x)的表达式,并写出其定义域.
(Ⅰ)解:依题意f(0)=0,又由f(x1)=1,当0≤y≤1时,函数y=f(x)的图象是斜率为b0=1的线段,故由![]() =1得x1=1.
=1得x1=1.
又由f(x2)=2,当1≤y≤2时,函数y=f(x)的图象是斜率为b的线段,
故由![]() =b,
=b,
即x2-x1=![]() 得x2=1+
得x2=1+![]() .
.
记x0=0.由函数y=f(x)图象中第n段线段的斜率为bn-1,故得![]() =bn-1.
=bn-1.
又f(xn)=n,f(xn-1)=n-1;
∴xn-xn-1=(![]() )n-1,n=1,2,….
)n-1,n=1,2,….
由此知数列{xn-xn-1}为等比数列,其首项为1,公比为![]() .
.
因b≠1,得xn=![]() =1+
=1+![]() +…+
+…+![]() =
= ,即xn=
,即xn=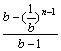
(Ⅱ)解:由(Ⅰ)知xn=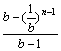 当b>1时,
当b>1时,![]()
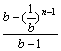 =
=![]()
当0<b<1时,n→∞,xn也趋向于无穷大,limxn不存在
(Ⅲ)解:由(Ⅰ)知:当0≤y≤1时,y=x,即当0≤x≤1时,f(x)=x;
当n≤y≤n+1即xn≤xn+1,由(Ⅰ)可知,
f(x)=n+bn(x-xn)(n=1,2,3,…)
由(Ⅱ)知:当b>1时,y=f(x)的定义域为[0,![]() ).
).
当0<b<1时,y=f(x)的定义域为[0,+∞).
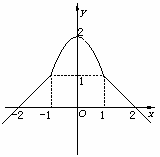
图1-30

练习册系列答案
相关题目