题目内容
在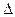 ABC中,角A、B、C的对边长分别是a、b、c,若
ABC中,角A、B、C的对边长分别是a、b、c,若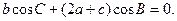
(I)求内角B的大小;
(Ⅱ)若b=2,求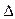 ABC面积的最大值
ABC面积的最大值
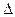 ABC中,角A、B、C的对边长分别是a、b、c,若
ABC中,角A、B、C的对边长分别是a、b、c,若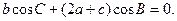
(I)求内角B的大小;
(Ⅱ)若b=2,求
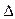 ABC面积的最大值
ABC面积的最大值(I)解法一:
∵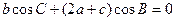 ,由正弦定理得:
,由正弦定理得:
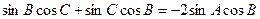 ,
,
即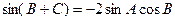 .………………2分
.………………2分
在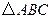 中,
中,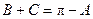 ,
,
∴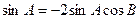 ,
,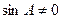 ………………3分
………………3分
∴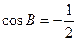 ,∴
,∴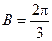 .………………5分
.………………5分
 解法二:
解法二:
因为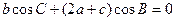 ,由余弦定理
,由余弦定理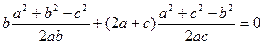 ,
,
化简得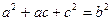 ,……………2分
,……………2分
又余弦定理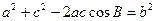 ,……………3分
,……………3分
所以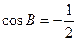 ,又
,又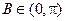 ,有
,有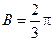 .……………5分
.……………5分
(II)解法一:
∵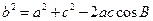 ,∴
,∴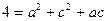 ,……………6分
,……………6分
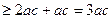 .
.
∴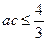 ,………………8分
,………………8分
∴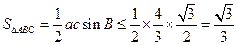 .………………9分
.………………9分
当且仅当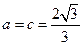 时取得等号.……………………10分
时取得等号.……………………10分
解法二:
由正弦定理知: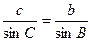 ,
,

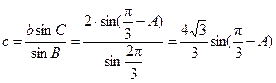 .………………6分
.………………6分
∴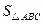
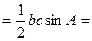
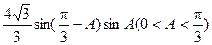 ,
,
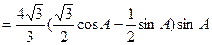
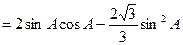
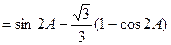
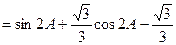
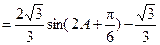 ,………………8分
,………………8分
∵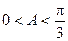 ,∴
,∴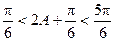 ,
,
∴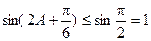 ,………………9分
,………………9分
∴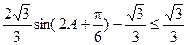 ,
,
即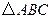 的面积
的面积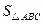 的最大值是
的最大值是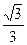 .………………10分
.………………10分
∵
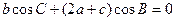 ,由正弦定理得:
,由正弦定理得: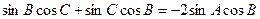 ,
,即
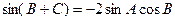 .………………2分
.………………2分在
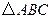 中,
中,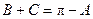 ,
,∴
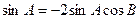 ,
,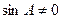 ………………3分
………………3分∴
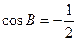 ,∴
,∴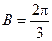 .………………5分
.………………5分 解法二:
解法二:因为
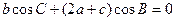 ,由余弦定理
,由余弦定理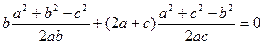 ,
,化简得
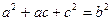 ,……………2分
,……………2分又余弦定理
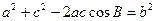 ,……………3分
,……………3分所以
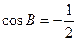 ,又
,又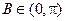 ,有
,有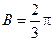 .……………5分
.……………5分(II)解法一:
∵
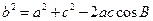 ,∴
,∴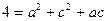 ,……………6分
,……………6分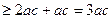 .
.∴
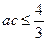 ,………………8分
,………………8分∴
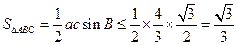 .………………9分
.………………9分当且仅当
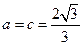 时取得等号.……………………10分
时取得等号.……………………10分解法二:
由正弦定理知:
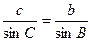 ,
,
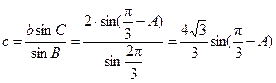 .………………6分
.………………6分∴
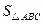
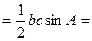
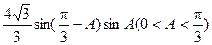 ,
,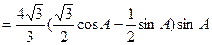
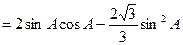
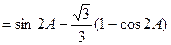
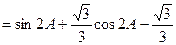
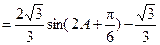 ,………………8分
,………………8分 ∵
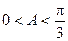 ,∴
,∴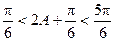 ,
,∴
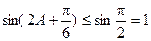 ,………………9分
,………………9分∴
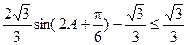 ,
,即
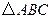 的面积
的面积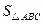 的最大值是
的最大值是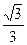 .………………10分
.………………10分略

练习册系列答案
相关题目
 ,
, ),
), ∈
∈ .
. =
= ,求角
,求角 =-1,求
=-1,求 的值.
的值.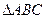 的角
的角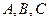 所对的边分别是
所对的边分别是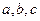 ,设向量
,设向量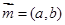 ,
,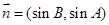 ,
,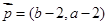 .
.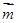 //
//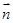 ,求证:
,求证: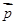 ,边
,边 长
长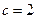 ,
,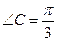 ,求
,求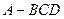 中,侧棱
中,侧棱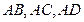 两两互相垂直,
两两互相垂直,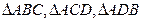 面积
面积 分别为
分别为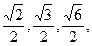 则三棱锥
则三棱锥 ABC的三边
ABC的三边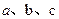 和面积
和面积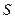 满足:
满足: 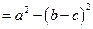 ,且
,且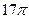 ,则面积
,则面积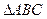 的外接圆半径为
的外接圆半径为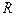 ,且已知
,且已知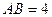 ,
,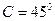 ,则
,则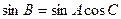 ,其中A、B
,其中A、B 、C是△ABC的三内角,则△ABC是 三角形。
、C是△ABC的三内角,则△ABC是 三角形。