题目内容
下列命题中不正确的命题个数是
①若A、B、C、D是空间任意四点,则有 +
+ +
+ +
+ =0;
=0;
②|a|-|b|=|a+b|是a、b共线的充要条件;
③若a、b共线,则a与b所在直线平行;
④对空间任意点O与不共线的三点A、B、C,若 =x
=x +y
+y +z
+z (其中x、y、z∈R),则P、A、B、C四点共面.
(其中x、y、z∈R),则P、A、B、C四点共面.
- A.1
- B.2
- C.3
- D.4
C
分析:①由向量的运算法则知正确
②两边平方,利用向量的平方等于向量模的平方,得出两向量反向.
③向量共线的几何意义知所在的线平行或重合.
④利用空间向量的基本定理知错.
解答:易知只有①是正确的,
对于②,|a|-|b|=|a+b|? =
= ?
? ?
? 反向,故②错.
反向,故②错.
对于③ 共线,则它们所在直线平行或重合
共线,则它们所在直线平行或重合
对于④,若O∉平面ABC,则 、
、 、
、 不共面,由空间向量基本定理知,P可为空间任一点,所以P、A、B、C四点不一定共面.
不共面,由空间向量基本定理知,P可为空间任一点,所以P、A、B、C四点不一定共面.
故选C.
点评:本题考查向量的运算法则、向量模的平方等于向量的平方、向量的几何意义、空间向量基本定理.
分析:①由向量的运算法则知正确
②两边平方,利用向量的平方等于向量模的平方,得出两向量反向.
③向量共线的几何意义知所在的线平行或重合.
④利用空间向量的基本定理知错.
解答:易知只有①是正确的,
对于②,|a|-|b|=|a+b|?
 =
= ?
? ?
? 反向,故②错.
反向,故②错.对于③
 共线,则它们所在直线平行或重合
共线,则它们所在直线平行或重合对于④,若O∉平面ABC,则
 、
、 、
、 不共面,由空间向量基本定理知,P可为空间任一点,所以P、A、B、C四点不一定共面.
不共面,由空间向量基本定理知,P可为空间任一点,所以P、A、B、C四点不一定共面.故选C.
点评:本题考查向量的运算法则、向量模的平方等于向量的平方、向量的几何意义、空间向量基本定理.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 是幂函数;
是幂函数;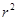 来刻画回归效果,
来刻画回归效果, 服从正态分布N(0,1),若
服从正态分布N(0,1),若 ,则
,则 ;
;
 与
与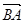 的长度相等
B.两个相等向量若起点相同,则终点必相同
的长度相等
B.两个相等向量若起点相同,则终点必相同