题目内容
已知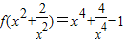
，则函数f（x）的最小值是（ ）A．2
B．3
C．-2
D．-5
【答案】分析：由题意设t=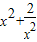
，利用基本不等式求出t的范围，并表示出
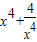，再代入原函数求出解析式，再由二次函数的单调性求出函数的最小值．
解答：解：由题意设t=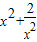
，则
，
∵
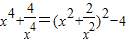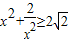（当且仅当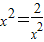
时取等号），∴t
，
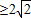代入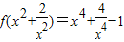
得，f（t）=t2-5，
∴f（x）=x2-5，且x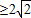
，
∴函数f（x）的最小值是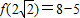
=3，
故选B．
点评：本题考查了换元法求函数解析式，以及基本不等式和二次函数的性质求最值问题，注意换元后一定要求出所换的未知数的范围，即函数的定义域．
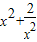，利用基本不等式求出t的范围，并表示出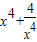，再代入原函数求出解析式，再由二次函数的单调性求出函数的最小值．解答：解：由题意设t=
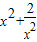，则，∵
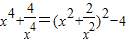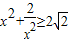（当且仅当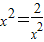时取等号），∴t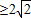，代入
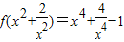得，f（t）=t2-5，∴f（x）=x2-5，且x
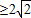，∴函数f（x）的最小值是
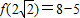=3，故选B．
点评：本题考查了换元法求函数解析式，以及基本不等式和二次函数的性质求最值问题，注意换元后一定要求出所换的未知数的范围，即函数的定义域．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
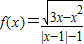，则函数f（x）的定义域为 ．
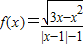，则函数f（x）的定义域为（ ）
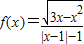，则函数f（x）的定义域为（ ）
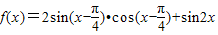，则函数f（x）得最小正周期是 ．