题目内容
函数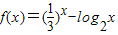 ,正实数a,b,c成公比大于1的等比数列,且满足f(a)•f(b)•f(c)<0,若x是方程f(x)=0的解,那么下列不等式中不可能成立的是( )
,正实数a,b,c成公比大于1的等比数列,且满足f(a)•f(b)•f(c)<0,若x是方程f(x)=0的解,那么下列不等式中不可能成立的是( )A.x<a
B.x>b
C.x<c
D.x>c
【答案】分析:由于函数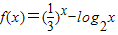 在其定义域(0,+∞)上是减函数,由条件可得0<a<b<c,且 f(c)<0,f(a)>0,再由x是方程f(x)=0的解,即f(x)=0,故有a<x<c,由此得出结论.
在其定义域(0,+∞)上是减函数,由条件可得0<a<b<c,且 f(c)<0,f(a)>0,再由x是方程f(x)=0的解,即f(x)=0,故有a<x<c,由此得出结论.
解答:解:由于函数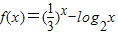 在其定义域(0,+∞)上是减函数,
在其定义域(0,+∞)上是减函数,
∵正实数a,b,c成公比大于1的等比数列,
∴0<a<b<c.
∵f(a)f(b)f(c)<0,
则f(a)<0,f(b)<0,f(c)<0,或者f(a)>0,f(b)>0,f(c)<0,
综合以上两种可能,恒有 f(c)<0,f(a)>0.
再由x是方程f(x)=0的解,即f(x)=0,故有 a<x<c,
故x0 >c 不可能成立,
故选D.
点评:本题主要考查函数的零点与方程的根的关系,等比数列的定义和性质,属于中档题.
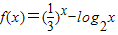 在其定义域(0,+∞)上是减函数,由条件可得0<a<b<c,且 f(c)<0,f(a)>0,再由x是方程f(x)=0的解,即f(x)=0,故有a<x<c,由此得出结论.
在其定义域(0,+∞)上是减函数,由条件可得0<a<b<c,且 f(c)<0,f(a)>0,再由x是方程f(x)=0的解,即f(x)=0,故有a<x<c,由此得出结论.解答:解:由于函数
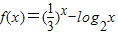 在其定义域(0,+∞)上是减函数,
在其定义域(0,+∞)上是减函数,∵正实数a,b,c成公比大于1的等比数列,
∴0<a<b<c.
∵f(a)f(b)f(c)<0,
则f(a)<0,f(b)<0,f(c)<0,或者f(a)>0,f(b)>0,f(c)<0,
综合以上两种可能,恒有 f(c)<0,f(a)>0.
再由x是方程f(x)=0的解,即f(x)=0,故有 a<x<c,
故x0 >c 不可能成立,
故选D.
点评:本题主要考查函数的零点与方程的根的关系,等比数列的定义和性质,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
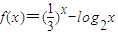 ,正实数a、b、c满足f(c)<0<f(a)<f(b).,若实数d是函数f(x)的一个零点,那么下列5个判断:①d<a;②d>b;③d<c;④c<a;⑤a<b.其中可能成立的个数为( )
,正实数a、b、c满足f(c)<0<f(a)<f(b).,若实数d是函数f(x)的一个零点,那么下列5个判断:①d<a;②d>b;③d<c;④c<a;⑤a<b.其中可能成立的个数为( )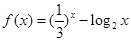 ,正实数a,b,c满足
,正实数a,b,c满足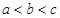 且
且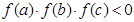 。
。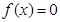 的一个解,那么下列四个判断:①
的一个解,那么下列四个判断:①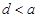 ;②
;②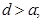 ③
③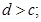 ④
④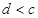 中有可能成立的个数为( )
中有可能成立的个数为( )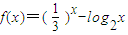 ,正实数a、b、c成公差为正数的等差数列,满足f (a) f (b) f (c)<0,且实数d是方程f (x)=0的一个解.给出下列四个不等式:①d<a,②d>b,③d<c,④d>c,其中有可能成立的不等式的序号是 .
,正实数a、b、c成公差为正数的等差数列,满足f (a) f (b) f (c)<0,且实数d是方程f (x)=0的一个解.给出下列四个不等式:①d<a,②d>b,③d<c,④d>c,其中有可能成立的不等式的序号是 .