题目内容
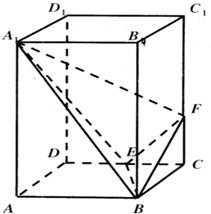 在长方体ABCD-A1B1ClDl中,已知AB=4,BC=2,CCl=5,E,F分别是CD,CCl上的点,A1F⊥平面BEF,
在长方体ABCD-A1B1ClDl中,已知AB=4,BC=2,CCl=5,E,F分别是CD,CCl上的点,A1F⊥平面BEF,(I)求CE,CF的长;
(Ⅱ)若CF>2,求二面角A1-BE-F的余弦值.
分析:(I)由题意画出一图形,因A1F⊥平面BEF,进而得到A1F⊥BE,在有线线垂直的到相似的三角形,得到CE与CE的长度;
(II)利用图形利用二面角平面角的概念找到二面角的平面角,在三角形中求解出二面角的三角函数值.
(II)利用图形利用二面角平面角的概念找到二面角的平面角,在三角形中求解出二面角的三角函数值.
解答: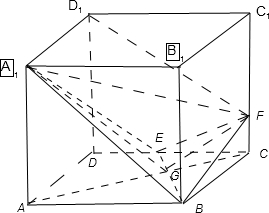 解:由题意做出图形:
解:由题意做出图形:
(I)连接AC,D1F,
∵A1F⊥平面BEF,∴A1F⊥BE,
又BE⊥CF∴BE⊥平面A1ACF,
∴BE⊥AC∴△BCE∽△ABE,
∴
=
?CE=1
∵EF⊥A1F,EF⊥A1D1,EF⊥平面A1D1F∴EF⊥D1F∴
=
?CFCE=1或4
(II)∵CF>2∴CF=4 设AC与BE交与点G,则AG⊥BE,FG⊥BE∴∠A1GF就是A1-BE-F的平面角AG=
,CG=
,A1G=
,FG=
∴cos∠A1GF=
=
∴二面角A1-BE-F的余弦值为
.
故答案为:(I)CE=1,CF=1或4,(II)
.
 解:由题意做出图形:
解:由题意做出图形:(I)连接AC,D1F,
∵A1F⊥平面BEF,∴A1F⊥BE,
又BE⊥CF∴BE⊥平面A1ACF,
∴BE⊥AC∴△BCE∽△ABE,
∴
| CE |
| 2 |
| 2 |
| 4 |
∵EF⊥A1F,EF⊥A1D1,EF⊥平面A1D1F∴EF⊥D1F∴
| 1 |
| CF |
| 5-CF |
| 4 |
(II)∵CF>2∴CF=4 设AC与BE交与点G,则AG⊥BE,FG⊥BE∴∠A1GF就是A1-BE-F的平面角AG=
| 8 | ||
|
| 2 | ||
|
3
| ||
|
2
| ||
|
∴cos∠A1GF=
| FG |
| A1G |
| 2 |
| 3 |
| 2 |
| 3 |
故答案为:(I)CE=1,CF=1或4,(II)
| 2 |
| 3 |
点评:此题重点考查了利用线线垂直判断线面垂直进而得到线线垂直,还考查了利用三角形的相似解出线段长度,此外在第二问中海考查了利用二面角的平面角的概念找出二面角的平面角,及在三角形中解出平面角的大小.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 在长方体ABCD-A'B'C'D'中,AB=
在长方体ABCD-A'B'C'D'中,AB= 如图,在长方体ABCD-A′B′C′D′中,用截面截下一个棱锥C-A′DD′,求棱锥C-A′DD′的体积与剩余部分的体积之比.
如图,在长方体ABCD-A′B′C′D′中,用截面截下一个棱锥C-A′DD′,求棱锥C-A′DD′的体积与剩余部分的体积之比. (2013•上海) 如图,在长方体ABCD-A′B′C′D′中,AB=2,AD=1,AA′=1.证明直线BC′平行于平面D′AC,并求直线BC′到平面D′AC的距离.
(2013•上海) 如图,在长方体ABCD-A′B′C′D′中,AB=2,AD=1,AA′=1.证明直线BC′平行于平面D′AC,并求直线BC′到平面D′AC的距离. (2009•青浦区二模)(理)在长方体ABCD-A'B'C'D'中,AB=2,AD=1,AA'=1.
(2009•青浦区二模)(理)在长方体ABCD-A'B'C'D'中,AB=2,AD=1,AA'=1. 已知在长方体ABCD-A′B′C′D′中,点E为棱CC′上任意一点,AB=BC=2,CC′=1.
已知在长方体ABCD-A′B′C′D′中,点E为棱CC′上任意一点,AB=BC=2,CC′=1.