题目内容
已知离心率为
的椭圆的中心在原点,焦点在x轴上,双曲线以椭圆的长轴为实轴,短轴为虚轴,且焦距为2
.
(I)求椭圆及双曲线的方程;
(Ⅱ)设椭圆的左、右顶点分别为A,B,在第二象限内取双曲线上一点P,连结BP交椭圆于点M,连结PA并延长交椭圆于点N,若
=
.求四边形ANBM的面积.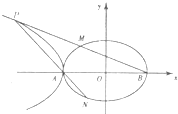
| 4 |
| 5 |
| 34 |
(I)求椭圆及双曲线的方程;
(Ⅱ)设椭圆的左、右顶点分别为A,B,在第二象限内取双曲线上一点P,连结BP交椭圆于点M,连结PA并延长交椭圆于点N,若
| BM |
| MP |

(I)设椭圆方程为
+
=1(a>b>0).
则根据题意,双曲线的方程为
-
=1,且满足
,解方程组得
∴椭圆的方程为
+
=1,双曲线的方程
-
=1;
(Ⅱ)由(I)得A(-5,0),B(5,0),|AB|=10.
设M(x0,y0),则由
=
得M为BP的中点,所以P点坐标为(2x0-5,2y0),
将M、P坐标代入椭圆和双曲线方程,得
,
消去y0,得2x02-5x0-25=0
解之得x0=-
或x0=5(舍)
所以y0=
,由此可得M(-
,
),
所以P(-10,3
).
当P为(-10,3
)时,直线PA的方程是y=
(x+5)
即y=-
(x+5).
代入
+
=1,得2x2+15x+25=0
所以x=-
或-5(舍),
所以xN=-
,xN=xM,MN⊥x轴.
所以SANBM=2S△ANB=2×10×
×
=15
.
| x2 |
| a2 |
| y2 |
| b2 |
则根据题意,双曲线的方程为
| x2 |
| a2 |
| y2 |
| b2 |
|
|
∴椭圆的方程为
| x2 |
| 25 |
| y2 |
| 9 |
| x2 |
| 25 |
| y2 |
| 9 |
(Ⅱ)由(I)得A(-5,0),B(5,0),|AB|=10.
设M(x0,y0),则由
| BM |
| MP |
将M、P坐标代入椭圆和双曲线方程,得
|
消去y0,得2x02-5x0-25=0
解之得x0=-
| 5 |
| 2 |
所以y0=
3
| ||
| 2 |
| 5 |
| 2 |
3
| ||
| 2 |
所以P(-10,3
| 3 |
当P为(-10,3
| 3 |
3
| ||
| -10+5 |
即y=-
3
| ||
| 5 |
代入
| x2 |
| 25 |
| y2 |
| 9 |
所以x=-
| 5 |
| 2 |
所以xN=-
| 5 |
| 2 |
所以SANBM=2S△ANB=2×10×
3
| ||
| 2 |
| 1 |
| 2 |
| 3 |

练习册系列答案
相关题目
 (2009•日照一模)已知离心率为
(2009•日照一模)已知离心率为