题目内容
已知函数f(x)=ax3+bx2+cx+d(a,b,c,d∈R),且函数f(x)的图象关于原点对称,其图象在x=3的切线方程为8x-y-18=0.(Ⅰ)求f(x)的解析式;
(Ⅱ)是否存在区间[a,b],使得函数g(x)的定义域和值域均为[a,b],且解析式与f(x)的解析式相同?若存在,求出这样的一个区间[a,b];若不存在,请说明理由.
答案:解:(Ⅰ)由已知有f(x)是奇函数,所以b=d=0.
又在x=3的切线方程为8x-y-18=0,
所以切点为(3,6),且f′(x)|x=3=8.
而f′(x)=3ax2+c,所以有![]()
即得a=![]() ,c=-1.故f(x)=
,c=-1.故f(x)=![]() x3-x.
x3-x.
(Ⅱ)解方程组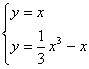 ,得x1=0,x2=
,得x1=0,x2=![]() ,x3=
,x3=![]() ,且f(
,且f(![]() )=
)=![]() ,f(
,f(![]() )=
)=![]() .
.
又f′(x)=x2-1,令f′(x)=x2-1=0,得x=±1.
所以f′(x)在(-![]() ,-1)和(1,+∞)上都有f′(x)>0,f′(x)在(-1,1)上f′(x)<0,故f(x)在(-∞,-1)和(1,+∞)上都为增函数,在(-1,1)上为减函数.
,-1)和(1,+∞)上都有f′(x)>0,f′(x)在(-1,1)上f′(x)<0,故f(x)在(-∞,-1)和(1,+∞)上都为增函数,在(-1,1)上为减函数.
所以f(x)在x=1处有极小值![]() ,在x=-1处有极大值
,在x=-1处有极大值![]() .
.
而极小值f(1)=![]() >
>![]() =f(
=f(![]() ),
),
极大值f(-1)=![]() <
<![]() =f(
=f(![]() ),
),
所以f(x)max=![]() ,f(x)min=
,f(x)min=![]() .
.
所以f(x)在区间[![]() ,
,![]() ]上的值域为[
]上的值域为[![]() ,
,![]() ].
].
综合以上得:存在区间[a,b]=[![]() ,
,![]() ]符合要求.
]符合要求.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
已知函数f(x)=a-
,若f(x)为奇函数,则a=( )
| 1 |
| 2x+1 |
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |