题目内容
(本小题满分12分)
一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(1)从袋中随机取两个球,求取出的球的编号之和不大于4的概率;
(2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求n<m+2的概率.
【答案】
(1)从袋中随机取两个球,其一切可能的结果组成的基本事件有1和2,1和3,1和4,2和3,2和4,3和4,共6个.
从袋中取出的球的编号之和不大于4的事件共有1和2,1和3,共两个.
因此所求事件的概率P=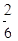 =
=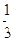 .
………6分
.
………6分
(2)先从袋中随机取一个球,记下编号为m,放回后,再从袋中随机取一个球,记下编号为n,其一切可能的结果(m,n)有:(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4),共16个.
又满足条件n≥m+2的事件为(1,3),(1,4),(2,4),共3个,
所以满足条件n≥m+2的事件的概率为P1=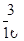 .
.
故满足条件n<m+2的事件的概率为1-P1=1-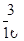 =
=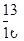 .
……12分
.
……12分
【解析】(1)本小题属于古典概型.先求出一切可能结果有6种,然后再求出事件包含的基本结果数2,则概率为2/6=1/3.
(2)与(1)属于同一类型.总的结果有16个,满足n≥m+2的基本结果有3个,则概率为3/16.那么其对立事件n<m+2的事件的概率为13/16.

练习册系列答案
相关题目