题目内容
一个四棱锥S-ABCD的底面是边长为a的正方形,且SA=a,SB=SD= a。
a。
 a。
a。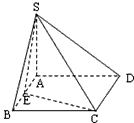
(1)求证:SA⊥平面ABCD;
(2)若SC为四棱锥中最长的侧棱,点E为AB的中点。求直线SE与平面SAC所成角的正弦值。
(2)若SC为四棱锥中最长的侧棱,点E为AB的中点。求直线SE与平面SAC所成角的正弦值。
解:(1)∵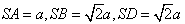
∴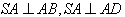
∴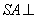 平面
平面 。
。
(2)作EF⊥AC交于F,连接SF,
易证EF⊥SA
∴EF⊥平面SAC
∴∠ESF是直线SE与平面SAC所成角。
EF= ,SE=
,SE=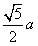
∴ 。
。
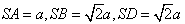
∴
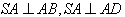
∴
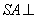 平面
平面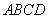 。
。(2)作EF⊥AC交于F,连接SF,
易证EF⊥SA
∴EF⊥平面SAC
∴∠ESF是直线SE与平面SAC所成角。
EF=
 ,SE=
,SE=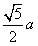
∴
 。
。
练习册系列答案
相关题目