题目内容
函数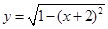 图像上存在不同的三点到原点的距离构成等比数列,则以下
图像上存在不同的三点到原点的距离构成等比数列,则以下
不可能成为公比的数是( )
A.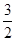 | B.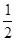 | C.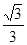 | D.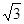 |
B
解析试题分析:函数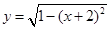 图象上的点到原点的距离的最小值为1,最大值为3,故
图象上的点到原点的距离的最小值为1,最大值为3,故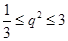 ,即
,即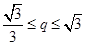 ,而
,而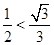 ,因此选B.
,因此选B.
考点:等比数列的性质.

练习册系列答案
相关题目
设等比数列{an}的前n项为Sn,若 则数列{ an}的公比为q为( )
则数列{ an}的公比为q为( )
| A.2 | B.3 | C.4 | D.5 |
等比数列 的前n项和为
的前n项和为 ,已知
,已知 ,则
,则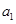 =( )
=( )
A.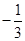 | B.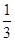 | C.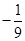 | D.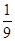 |
已知在数列 中,
中,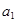 =1,
=1,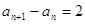 (
(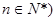 ,则
,则 为
为
A.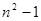 | B.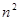 | C.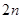 | D.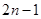 |
等比数列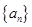 中,
中,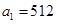 ,公比
,公比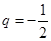 ,用
,用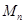 表示它的前
表示它的前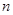 项之积,即
项之积,即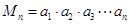 ,则数列
,则数列 中的最大项是( )
中的最大项是( )
A.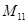 | B.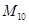 | C.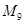 | D. |
若等比数列{an}满足a2+a4=20,a3+a5=40,前100项和S100=( )
| A.2101 |
| B.2101+2 |
| C.2100-2 |
| D.2100 |
已知数列{an}满足a1>0,且an+1=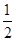 an,则数列{an}是( )
an,则数列{an}是( )
| A.递增数列 |
| B.递减数列 |
| C.常数列 |
| D.摆动数列 |
设等比数列{an}中,前n项和为Sn,已知S3=8,S6=7,则a7+a8+a9=( )
A. | B.- | C.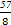 | D.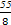 |
 元的一年定期储蓄。若年利率为
元的一年定期储蓄。若年利率为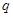 保持不变,且每年到期的存款本息均自动转为新的一年定期储蓄,到2014年1月1日,甲去银行不再存款,而是将所有存款的本息全部取回,则取回的金额是( )元.
保持不变,且每年到期的存款本息均自动转为新的一年定期储蓄,到2014年1月1日,甲去银行不再存款,而是将所有存款的本息全部取回,则取回的金额是( )元.


