题目内容
如图,多面体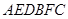 的直观图及三视图如图所示,
的直观图及三视图如图所示,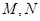 分别为
分别为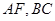 的中点.
的中点.
(1)求证: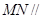 平面
平面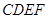 ;
;
(2)求多面体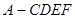 的体积.
的体积.
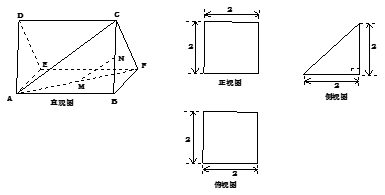
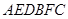 的直观图及三视图如图所示,
的直观图及三视图如图所示,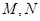 分别为
分别为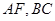 的中点.
的中点.(1)求证:
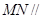 平面
平面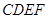 ;
;(2)求多面体
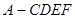 的体积.
的体积.
(1)证明:见解析;(2)多面体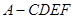 的体积
的体积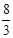 .
.
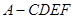 的体积
的体积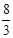 .
. 试题分析: (1)由多面体
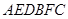 的三视图知,三棱柱
的三视图知,三棱柱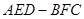 中,底面
中,底面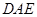 是等腰
是等腰直角三角形,
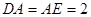 ,
,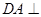 平面
平面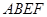 ,侧面
,侧面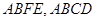 都是边长为
都是边长为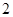 的正方形.
的正方形.连结
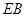 ,则
,则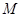 是
是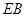 的中点,由三角形中位线定理得
的中点,由三角形中位线定理得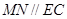 ,得证.
,得证.(2)利用
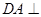 平面
平面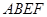 ,得到
,得到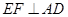 ,
,再据
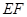 ⊥
⊥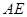 ,得到
,得到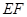 ⊥平面
⊥平面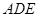 ,从而可得:四边形
,从而可得:四边形 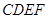 是矩形,且侧面
是矩形,且侧面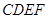 ⊥平面
⊥平面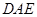 .
.取
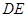 的中点
的中点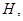 得到
得到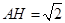 ,且
,且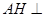 平面
平面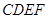 .利用体积公式计算.
.利用体积公式计算.所以多面体
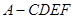 的体积
的体积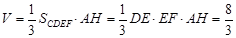 . 12分
. 12分试题解析: (1)证明:由多面体
 的三视图知,三棱柱
的三视图知,三棱柱 中,底面
中,底面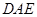 是等腰
是等腰直角三角形,
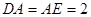 ,
,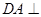 平面
平面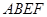 ,侧面
,侧面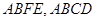 都是边长为
都是边长为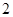 的
的正方形.连结
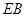 ,则
,则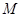 是
是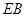 的中点,
的中点,在△
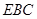 中,
中,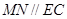 ,
, 且
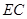
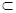 平面
平面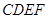 ,
,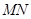
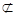 平面
平面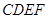 ,
,∴
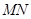 ∥平面
∥平面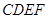 . 6分
. 6分
(2) 因为
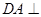 平面
平面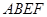 ,
,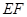
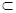 平面
平面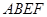 ,
,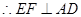 ,
,又
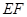 ⊥
⊥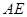 ,所以,
,所以,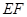 ⊥平面
⊥平面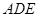 ,
,∴四边形
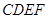 是矩形,且侧面
是矩形,且侧面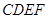 ⊥平面
⊥平面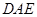 8分
8分取
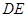 的中点
的中点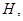
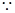
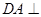
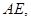
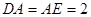 ,
,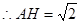 ,且
,且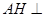 平面
平面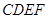 . 10分
. 10分所以多面体
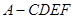 的体积
的体积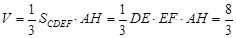 . 12分
. 12分
练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 中,
中, 平面
平面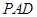 ,
, ,
, ,
, 是
是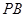 的中点,
的中点, 是
是 上的点且
上的点且 ,
, 为△
为△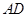 边上的高.
边上的高.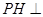 平面
平面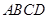 ;
; ,
, ,
, ,求三棱锥
,求三棱锥 的体积;
的体积;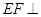 平面
平面 .
.
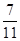
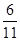
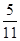
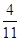
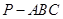 中,
中,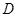 ,
,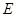 分别为
分别为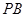 ,
,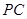 的中点,记三棱锥
的中点,记三棱锥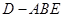 的体积为
的体积为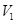 ,
,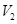 ,则
,则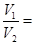 ________.
________.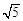 cm的圆面,球心到这个平面的距离是2cm,则球O的体积是( )
cm的圆面,球心到这个平面的距离是2cm,则球O的体积是( )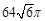 cm3
cm3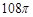 cm3
cm3