题目内容
【题目】已知函数f(x)= ![]() ax2+lnx,a∈R. (Ⅰ)若曲线y=f(x)与直线y=3x+b在x=1处相切,求实数a,b的值;
ax2+lnx,a∈R. (Ⅰ)若曲线y=f(x)与直线y=3x+b在x=1处相切,求实数a,b的值;
(Ⅱ)求函数y=f(x)的单调区间;
(Ⅲ)若a=0时,函数h(x)=f(x)+bx有两个不同的零点,求实数b的取值范围.
【答案】解:(Ⅰ)∵函数f(x)= ![]() ax2+lnx,x>0, ∴f′(x)=ax+
ax2+lnx,x>0, ∴f′(x)=ax+ ![]() ,
,
∵曲线y=f(x)与直线y=3x+b在x=1处相切,
∴f′(1)=a+1=3,
∴a=2,
∴f(1)=1+ln1=1,
∴1=3+b,
∴b=﹣2,
(Ⅱ)由(1)可得f′(x)=ax+ ![]() ,
,
当a≥0时,f′(x)=ax+ ![]() >0恒成立,
>0恒成立,
∴f(x)在(0,+∞)上单调递增,
当a<0时,令f′(x)=0,解得x= ![]() =
= ![]() ,
,
当x∈(0, ![]() )时,f′(x)>0,函数单调递增,
)时,f′(x)>0,函数单调递增,
当x∈( ![]() ,+∞)时,f′(x)<0,函数单调递减,
,+∞)时,f′(x)<0,函数单调递减,
(Ⅲ)a=0时,函数h(x)=f(x)+bx=lnx+bx
令m(x)=lnx,n(x)=﹣bx,
要使得h(x)有两个零点,即使得m(x)和n(x)图象有两个交点(如图),
容易求得m(x)和n(x)的切点为(e,1),
∴0<﹣b< ![]() ,即﹣
,即﹣ ![]() <b<0.
<b<0.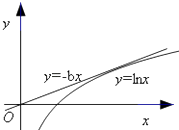
【解析】(Ⅰ)根据导数的几何意义即可求出k,b的值,(Ⅱ)先求导,再分类讨论,根据导数和函数的单调性关系即可求出.(Ⅲ)当a=0时,若函数h(x)有两个不同的零点,利用数形结合即可求b的取值范围;
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.

【题目】近年来,手机已经成为人们日常生活中不可缺少的产品,手机的功能也日趋完善,已延伸到了各个领域,如拍照,聊天,阅读,缴费,购物,理财,娱乐,办公等等,手机的价格差距也很大,为分析人们购买手机的消费情况,现对某小区随机抽取了200人进行手机价格的调查,统计如下:
年龄 价格 | 5000元及以上 | 3000元﹣4999元 | 1000元﹣2999元 | 1000元以下 |
45岁及以下 | 12 | 28 | 66 | 4 |
45岁以上 | 3 | 17 | 46 | 24 |
(Ⅰ)完成关于人们使用手机的价格和年龄的2×2列联表,再判断能否在犯错误的概率不超过0.025的前提下,认为人们使用手机的价格和年龄有关?
(Ⅱ)从样本中手机价格在5000元及以上的人群中选择3人调查其收入状况,设3人中年龄在45岁及以下的人数为随机变量X,求随机变量X的分布列及数学期望.
附K2= ![]()
P(K2≥k) | 0.05 | 0.025 | 0.010 | 0.001 |
k | 3.841 | 5.024 | 6.635 | 10.828 |