题目内容
已知:(1+tan10°)(1+tan35°)=2;(1+tan20°)(1+tan25°)=2;(1+tan30°)(1+tan15°)=2通过观察上述三个等式的规律,请你写出一般性的命题,并给出的证明.
【答案】分析:根据题意可得:若α+β=45°,则(1+tanα)(1+tanβ)=2.因为α+β=45°,所以tan(α+β)=tan45°=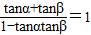 ,即tanα+tanβ=1-tanαtanβ,即可得到tanα+tanβ+tanαtanβ=1,进而得到答案.
,即tanα+tanβ=1-tanαtanβ,即可得到tanα+tanβ+tanαtanβ=1,进而得到答案.
解答:解:根据题意可得:若α+β=45°,则(1+tanα)(1+tanβ)=2.
因为α+β=45°,所以tan(α+β)=tan45°= ,即tanα+tanβ=1-tanαtanβ.
,即tanα+tanβ=1-tanαtanβ.
所以(1+tanα)(1+tanβ)=1+tanα+tanβ+tanαtanβ=2.
所以若α+β=45°,则(1+tanα)(1+tanβ)=2正确.
点评:解决此类问题的关键是熟练掌握归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想),(3)利用一个该生进行论证.
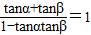 ,即tanα+tanβ=1-tanαtanβ,即可得到tanα+tanβ+tanαtanβ=1,进而得到答案.
,即tanα+tanβ=1-tanαtanβ,即可得到tanα+tanβ+tanαtanβ=1,进而得到答案.解答:解:根据题意可得:若α+β=45°,则(1+tanα)(1+tanβ)=2.
因为α+β=45°,所以tan(α+β)=tan45°=
 ,即tanα+tanβ=1-tanαtanβ.
,即tanα+tanβ=1-tanαtanβ.所以(1+tanα)(1+tanβ)=1+tanα+tanβ+tanαtanβ=2.
所以若α+β=45°,则(1+tanα)(1+tanβ)=2正确.
点评:解决此类问题的关键是熟练掌握归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想),(3)利用一个该生进行论证.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目