题目内容
若二次函数y=f（x）的图
象关于y轴对称，且1≤f（1）≤2，3≤f（2）≤4，求f（3）的范围.
解：设f（x）=ax2+c（a≠0），则f（1）=a+c，f（2）=4a+c.
又∵ f（3）=9a+c，故设
1f（1）+2f（2）=f（3），
则有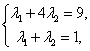
解得
∴ f（3）=
.
∵ 1≤f（1）≤2，3≤f（2）≤4，
∴ 5≤5f（1）≤10，24≤8f（2）≤32.
∴ 14≤8f（2）-5f（1）≤27.
∴ 
≤≤9，即≤f（3）≤9.
练习册系列答案
同步练习强化拓展系列答案
相关题目
若二次函数y=f（x）的图象过原点，且它的导数y=f′（x）的图象是经过第一、二、三象限的一条直线，则y=f（x）的图象顶点在（ ）
| A、第一象限 | B、第二象限 | C、第三象限 | D、第四象限 |