题目内容
函数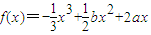 ,f′(x)是它的导函数.
,f′(x)是它的导函数.(Ⅰ)当b=1时,若f(x)在区间
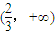 存在单调递增区间,求a的取值范围.
存在单调递增区间,求a的取值范围.(Ⅱ)当1≤x≤2时,f′(x)≥0恒成立,求a2+b2+10a的最小值.
【答案】分析:(Ⅰ)b=1时,函数的导函数为f′(x)=-x2+x+2a,若f(x)在区间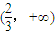 存在单调递增区间,应是在给定的区间内,有子区间使得导函数值大于0,然后借助于二次函数图象开口向下,对称轴一定列不等式求a的取值范围;
存在单调递增区间,应是在给定的区间内,有子区间使得导函数值大于0,然后借助于二次函数图象开口向下,对称轴一定列不等式求a的取值范围;
(Ⅱ)导函数仍然是二次函数,开口向下,在闭区间上大于等于0恒成立,只要两端点的函数值同时大于等于0即可,得到关于a、b的二次不等式组后,分析二元一次不等式所表示的平面区域,运用几何意义知:a2+b2+10a=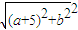 -25,最后求点(-5,0)到区域内最近点的距离.
-25,最后求点(-5,0)到区域内最近点的距离.
解答:解:(Ⅰ)当b=1时,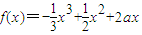 ,f′(x)=-x2+x+2a,若f(x)在区间
,f′(x)=-x2+x+2a,若f(x)在区间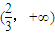 存在单调递增区间,则在区间
存在单调递增区间,则在区间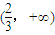 内存在子区间使得f′(x)=-x2+x+2a>0,
内存在子区间使得f′(x)=-x2+x+2a>0,
因导函数对应的图象是开口向下的抛物线,且对称轴方程为x= ,那么要使在区间
,那么要使在区间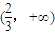 内存在子区间使得f′(x)=-x2+x+2a>0成立,
内存在子区间使得f′(x)=-x2+x+2a>0成立,
只需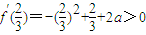 ,解得:
,解得: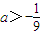 .
.
所以a的范围为{a|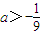 }.
}.
(Ⅱ)由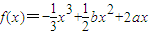 ,得f′(x)=-x2+bx+2a,导函数图象是开口向下的抛物线,要使当1≤x≤2时,f′(x)≥0恒成立,则
,得f′(x)=-x2+bx+2a,导函数图象是开口向下的抛物线,要使当1≤x≤2时,f′(x)≥0恒成立,则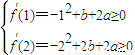
即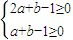
而a2+b2+10a=(a+5)2+b2-25=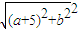 -25,二元一次不等式组
-25,二元一次不等式组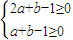 表示的平面区域内的动点(a,b)为(-1,3)时到定点(-5,0)的距离最小,
表示的平面区域内的动点(a,b)为(-1,3)时到定点(-5,0)的距离最小,
此时有(a2+b2+10a)min=(-1+5)2+32-25=0.
所以,满足当1≤x≤2时,f′(x)≥0恒成立的a2+b2+10a的最小值为0.
点评:本题第一问考查了运用导函数在区间内的符号判断原函数在区间内的单调性问题,解答的关键是理解f(x)在区间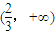 内存在单调递增区间的意义;第二问是基本的二次函数在区间内大于0恒成立问题,求最值时体现了数学转化思想和数形结合思想,同时训练了二元一次不等式所表示的平面区域问题,综合性强.
内存在单调递增区间的意义;第二问是基本的二次函数在区间内大于0恒成立问题,求最值时体现了数学转化思想和数形结合思想,同时训练了二元一次不等式所表示的平面区域问题,综合性强.
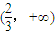 存在单调递增区间,应是在给定的区间内,有子区间使得导函数值大于0,然后借助于二次函数图象开口向下,对称轴一定列不等式求a的取值范围;
存在单调递增区间,应是在给定的区间内,有子区间使得导函数值大于0,然后借助于二次函数图象开口向下,对称轴一定列不等式求a的取值范围;(Ⅱ)导函数仍然是二次函数,开口向下,在闭区间上大于等于0恒成立,只要两端点的函数值同时大于等于0即可,得到关于a、b的二次不等式组后,分析二元一次不等式所表示的平面区域,运用几何意义知:a2+b2+10a=
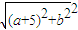 -25,最后求点(-5,0)到区域内最近点的距离.
-25,最后求点(-5,0)到区域内最近点的距离.解答:解:(Ⅰ)当b=1时,
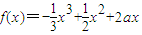 ,f′(x)=-x2+x+2a,若f(x)在区间
,f′(x)=-x2+x+2a,若f(x)在区间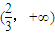 存在单调递增区间,则在区间
存在单调递增区间,则在区间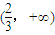 内存在子区间使得f′(x)=-x2+x+2a>0,
内存在子区间使得f′(x)=-x2+x+2a>0,因导函数对应的图象是开口向下的抛物线,且对称轴方程为x=
 ,那么要使在区间
,那么要使在区间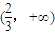 内存在子区间使得f′(x)=-x2+x+2a>0成立,
内存在子区间使得f′(x)=-x2+x+2a>0成立,只需
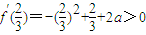 ,解得:
,解得: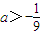 .
.所以a的范围为{a|
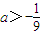 }.
}.(Ⅱ)由
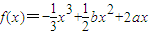 ,得f′(x)=-x2+bx+2a,导函数图象是开口向下的抛物线,要使当1≤x≤2时,f′(x)≥0恒成立,则
,得f′(x)=-x2+bx+2a,导函数图象是开口向下的抛物线,要使当1≤x≤2时,f′(x)≥0恒成立,则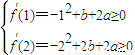
即
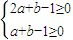
而a2+b2+10a=(a+5)2+b2-25=
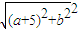 -25,二元一次不等式组
-25,二元一次不等式组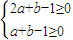 表示的平面区域内的动点(a,b)为(-1,3)时到定点(-5,0)的距离最小,
表示的平面区域内的动点(a,b)为(-1,3)时到定点(-5,0)的距离最小,此时有(a2+b2+10a)min=(-1+5)2+32-25=0.
所以,满足当1≤x≤2时,f′(x)≥0恒成立的a2+b2+10a的最小值为0.
点评:本题第一问考查了运用导函数在区间内的符号判断原函数在区间内的单调性问题,解答的关键是理解f(x)在区间
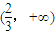 内存在单调递增区间的意义;第二问是基本的二次函数在区间内大于0恒成立问题,求最值时体现了数学转化思想和数形结合思想,同时训练了二元一次不等式所表示的平面区域问题,综合性强.
内存在单调递增区间的意义;第二问是基本的二次函数在区间内大于0恒成立问题,求最值时体现了数学转化思想和数形结合思想,同时训练了二元一次不等式所表示的平面区域问题,综合性强. 
练习册系列答案
相关题目