题目内容
设函数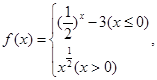 已知
已知 ,则实数
,则实数 的取值范围是( )
的取值范围是( )
A. | B. |
C. | D. |
B
解析试题分析:分段函数分段求解,需要分类讨论
i、当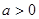 时,
时,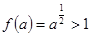
可以求得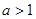
ii、当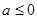 时,
时,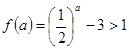
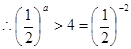
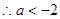
综上所述,实数 的取值范围是
的取值范围是
考点:本题表面看到的是考查分段函数问题,实质是对分类讨论思想的考查,内容还涉及到指数函数的单调性
点评:本题对分类讨论思想的考查比较细腻,考查知识点还涉及到指数函数单调性,实在难得。

练习册系列答案
相关题目
一水池有2个进水口,1个出水口,进出水速度如图甲、乙所示. 某天0点到6点,该水池的蓄水量如图丙所示.(至少打开一个水口)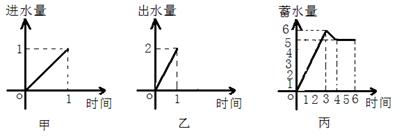
给出以下3个论断:①0点到3点只进水不出水;C②3点到4点不进水只出水;③4点到6点不进水不出水. 则正确论断的个数是( )
| A.0 | B. 1 | C. 2 | D. 3 |
已知函数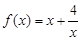 ,且当
,且当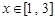 ,
,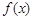 的值域是
的值域是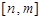 ,则
,则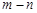 的值是
的值是
A.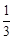 | B.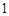 | C. | D.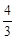 |
函数 是定义在R上的偶函数,当
是定义在R上的偶函数,当 时,
时, ,那么当
,那么当 时,
时, 的解析式是
的解析式是
A. | B. | C. | D.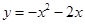 |
函数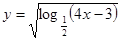 的定义域为 ( )
的定义域为 ( )
A.(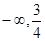 ) ) | B.(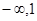 ] ] | C.(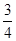 ,1] ,1] | D.(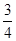 ,1) ,1) |
设集合 ,
, 则
则 ( )
( )
A. | B. | C. | D. |
设函数 ,则
,则 ( )
( )
A.在区间 内均有零点 内均有零点 |
B.在区间 内均无零点 内均无零点 |
C.在区间 内有零点,在区间 内有零点,在区间 内无零点 内无零点 |
D.在区间 内无零点,在区间 内无零点,在区间 内有零点 内有零点 |
已知偶函数 在区间
在区间 上单调递增,则满足不等式
上单调递增,则满足不等式 的
的 的取值范围是 ( )
的取值范围是 ( )
A.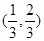 | B. | C.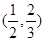 | D. |
 上的函数
上的函数 满足下列条件:①对任意的
满足下列条件:①对任意的 都有
都有 ;②若
;②若 ,都有
,都有 ;③
;③ 是偶函数,则下列不等式中正确的是()
是偶函数,则下列不等式中正确的是()


