题目内容
如果以原点为圆心的圆经过双曲线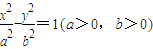 的焦点,而且它被该双曲线的右准线分成弧长为2:1的两段圆弧,那么该双曲线的离心率e等于( )
的焦点,而且它被该双曲线的右准线分成弧长为2:1的两段圆弧,那么该双曲线的离心率e等于( )A.
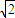
B.
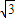
C.
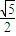
D.
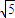
【答案】分析:由题设条件可知,圆的方程为x2+y2=c2,双曲线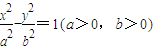 的右准线的方程是
的右准线的方程是 ,再由圆被该双曲线的右准线分成弧长为2:1的两段圆弧,可以推导出双曲线的离心率e.
,再由圆被该双曲线的右准线分成弧长为2:1的两段圆弧,可以推导出双曲线的离心率e.
解答:解:圆的方程为x2+y2=c2,右准线的方程是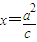 ,
,
它与圆在第一象限的交点记为P.由题意可得,
直线OP的方程为 .将
.将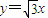 和
和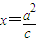
代入x2+y2=c2,有c2=2a2,即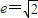 .故选A.
.故选A.
点评:本题考查圆的方程、双曲线的准线方程和离心率,解题要认真审题,仔细作答.
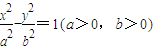 的右准线的方程是
的右准线的方程是 ,再由圆被该双曲线的右准线分成弧长为2:1的两段圆弧,可以推导出双曲线的离心率e.
,再由圆被该双曲线的右准线分成弧长为2:1的两段圆弧,可以推导出双曲线的离心率e.解答:解:圆的方程为x2+y2=c2,右准线的方程是
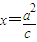 ,
,它与圆在第一象限的交点记为P.由题意可得,
直线OP的方程为
 .将
.将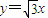 和
和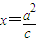
代入x2+y2=c2,有c2=2a2,即
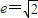 .故选A.
.故选A.点评:本题考查圆的方程、双曲线的准线方程和离心率,解题要认真审题,仔细作答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目