题目内容
设实部为正数的复数z,满足|z|=
,且复数(1+2i)z在复平面上对应的点在第一、三象限的角平分线,求复数z.
| 10 |
分析:设出复数z,由|z|=
,复数(1+2i)z的实部和虚部相等联立方程组即可求得复数z.
| 10 |
解答:解:设z=a+bi,a,b∈R,a>0,
由题意:a2+b2=10①
(1+2i)z=(1+2i)(a+bi)=a-2b+(2a+b)i,
得a-2b=2a+b②
①②联立,解得a=3,b=-1
得z=3-i.
由题意:a2+b2=10①
(1+2i)z=(1+2i)(a+bi)=a-2b+(2a+b)i,
得a-2b=2a+b②
①②联立,解得a=3,b=-1
得z=3-i.
点评:本题考查了复数的模,考查了复数的代数表示法和几何意义,是基础的运算题.

练习册系列答案
相关题目
 满足
满足 ,且
,且 在复平面上对应的点在第一、三象限的角平分线上.
在复平面上对应的点在第一、三象限的角平分线上.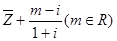 为纯虚数 , 求
为纯虚数 , 求 的值.
的值.