Question

（5分）设P₁，P₂，…P_n为平面α内的n个点，在平面α内的所有点中，若点P到点P₁，P₂，…P_n的距离之和最小，则称点P为P₁，P₂，…P_n的一个“中位点”，例如，线段AB上的任意点都是端点A，B的中位点，现有下列命题：

①若三个点A、B、C共线，C在线段AB上，则C是A，B，C的中位点；

②直角三角形斜边的中点是该直角三角形三个顶点的中位点；

③若四个点A、B、C、D共线，则它们的中位点存在且唯一；

④梯形对角线的交点是该梯形四个顶点的唯一中位点．

其中的真命题是　  　（写出所有真命题的序号）．

 

Answer 1

【答案】

①④

【解析】①若三个点A、B、C共线，C在线段AB上，根据两点之间线段最短，则C是A，B，C的中位点，正确；

②举一个反例，如边长为3，4，5的直角三角形ABC，此直角三角形的斜边的中点到三个顶点的距离之和为5+2.5=7.5，而直角顶点到三个顶点的距离之和为7，

∴直角三角形斜边的中点不是该直角三角形三个顶点的中位点；故错误；

③若四个点A、B、C、D共线，则它们的中位点是中间两点连线段上的任意一个点，故它们的中位点存在但不唯一；故错误；

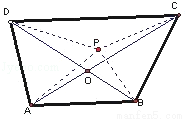
④如图，在梯形ABCD中，对角线的交点O，P是任意一点，则根据三角形两边之和大于第三边得

PA+PB+PC+PD≥AC+BD=OA+OB+OC+OD，

∴梯形对角线的交点是该梯形四个顶点的唯一中位点．正确．

故答案为：①④．