题目内容
已知数列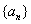 的前五项依次是
的前五项依次是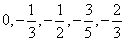 .
正数数列
.
正数数列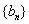 的前
的前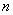 项和为
项和为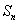 ,且
,且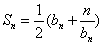 .
.
(I)写出符合条件的数列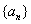 的一个通项公式;
的一个通项公式;
(II)求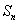 的表达式;
的表达式;
(III)在(I)、(II)的条件下,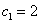 ,当
,当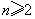 时,设
时,设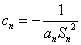 ,
,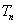 是数列
是数列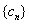 的前
的前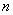 项和,且
项和,且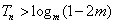 恒成立,求实数
恒成立,求实数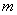 的取值范围.
的取值范围.
【答案】
解:(I)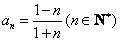 .
………………………………………2分
.
………………………………………2分
(II)因为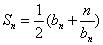 ,
,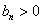 ,所以
,所以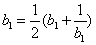 ,解得
,解得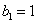 ,即
,即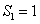 .
.
当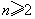 时,
时,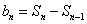 ,所以
,所以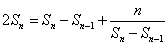 .
.
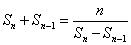 ,即
,即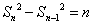 .
………………………………5分
.
………………………………5分
所以,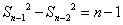 ,
,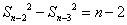 ,…,
,…,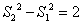 ,
,
累加,得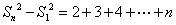 .
.
所以,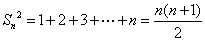 ,即
,即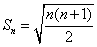 .
………………..8分
.
………………..8分
(III)在(I)、(II)的条件下,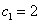 .
.
当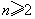 时,
时,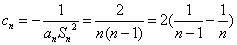 .
.
当 时,
时,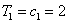 ;
;
当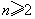 时,
时,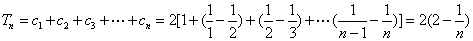 .
.
…………………………………………………….10分
因为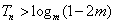 恒成立,即
恒成立,即 恒小于
恒小于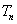 的最小值.
的最小值.
显然,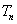 的最小值在
的最小值在 时取得,且最小值为2.
时取得,且最小值为2.
故有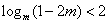 . …………………………………………………..12分
. …………………………………………………..12分
所以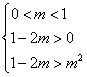 ① 或
① 或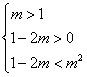 ②
②
解①得,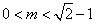 ,不等式组②无解.
,不等式组②无解.
故,实数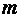 的取值范围是
的取值范围是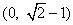 .
…………………………………….14分
.
…………………………………….14分

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
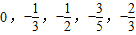 .正数数列{bn}的前n项和为Sn,且
.正数数列{bn}的前n项和为Sn,且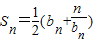 .
.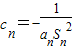 ,Tn是数列{cn}的前n项和,且Tn>logm(1-2m)恒成立,求实数m的取值范围.
,Tn是数列{cn}的前n项和,且Tn>logm(1-2m)恒成立,求实数m的取值范围.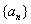 的前五项依次是
的前五项依次是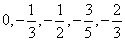 .
正数数列
.
正数数列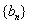 的前
的前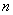 项和为
项和为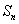 ,且
,且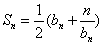 .
.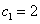 ,当
,当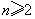 时,设
时,设 ,
,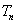 是数列
是数列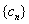 的前
的前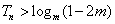 恒成立,求实数
恒成立,求实数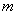 的取值范围.
的取值范围.