题目内容
已知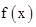 是二次函数,不等式
是二次函数,不等式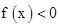 的解集是(0,5),且f(x)在区间[-1,4]上的最大值是12.
的解集是(0,5),且f(x)在区间[-1,4]上的最大值是12.
(1)求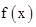 的解析式;
的解析式;
(2)是否存在自然数m,使得方程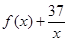 =0在区间(m,m+1)内有且只有两个不等的实数根?若存在,求出所有m的值;若不存在,请说明理由.
=0在区间(m,m+1)内有且只有两个不等的实数根?若存在,求出所有m的值;若不存在,请说明理由.
(1)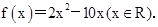
(2)存在唯一的自然数m=3,使得方程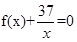 在区间(m,m+1)内有且只有两个不等的实数根.
在区间(m,m+1)内有且只有两个不等的实数根.
解析试题分析:(1)为求函数的解析式,可根据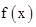 是二次函数,且
是二次函数,且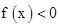 的解集是(0,5),
的解集是(0,5),
设出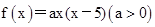 应用“待定系数法”.
应用“待定系数法”.
(2)首先注意到方程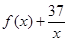 =0等价于方程
=0等价于方程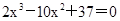 ,从而,可通过研究函数
,从而,可通过研究函数 达到解题目的.
达到解题目的.
具体地,通过“求导数、求驻点、讨论导数的正负、确定函数的单调区间”,认识方程的根分布情况.
试题解析:
(1)∵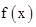 是二次函数,且
是二次函数,且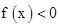 的解集是(0,5),
的解集是(0,5),
∴可设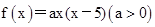 .
.
∴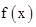 在区间[-1,4]上的最大值是
在区间[-1,4]上的最大值是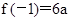 .
.
由已知,得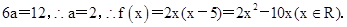 5分
5分
(2)方程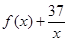 =0等价于方程
=0等价于方程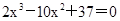
设
则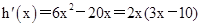 . 7分
. 7分
当x∈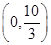 时,
时,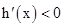 ,因此
,因此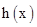 在此区间上是减少的;
在此区间上是减少的;
当x∈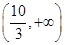 时,
时,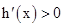 ,因此
,因此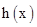 是在此区间上是增加的.
是在此区间上是增加的.
∵h(3)=1>0,h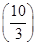 =
=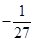 <0,h(4)=5>0, 10分
<0,h(4)=5>0, 10分
∴方程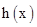 =0在区间
=0在区间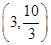 ,
,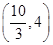 内分别有唯一实数根,而在区间(0,3),(4,+∞)内没有实数根,
内分别有唯一实数根,而在区间(0,3),(4,+∞)内没有实数根,
∴存在唯一的自然数m=3,使得方程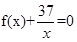 在区间(m,m+1)内有且只有两个不等的实数根. 12分
在区间(m,m+1)内有且只有两个不等的实数根. 12分
考点:待定系数法,应用导数研究函数的单调性,函数方程.

练习册系列答案
相关题目
 .
.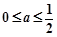 时,试讨论
时,试讨论 的单调性;
的单调性;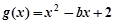 ,当
,当 时,若对任意
时,若对任意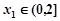 ,存在
,存在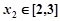 ,使
,使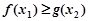 ,求实数
,求实数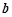 取值范围.
取值范围.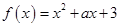 .
. 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,
,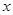 的取值范围.
的取值范围.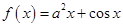 ,
,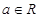 .
. 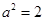 时,求
时,求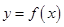 在
在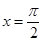 处的切线方程;
处的切线方程; 在
在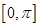 内单调递增,求
内单调递增,求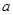 的取值范围.
的取值范围.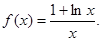
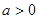 且函数
且函数 在区间
在区间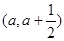 上存在极值,求实数
上存在极值,求实数 的取值范围;
的取值范围;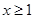 时,不等式
时,不等式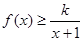 恒成立,求实数
恒成立,求实数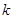 的取值范围.
的取值范围.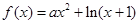 .
.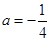 时,求函数
时,求函数 的单调区间;
的单调区间;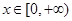 时,不等式
时,不等式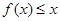 恒成立,求实数
恒成立,求实数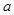 的取值范围.
的取值范围.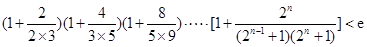 (
(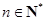 ,e是自然对数的底数).
,e是自然对数的底数).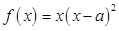 ,
,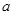 是大于零的常数.
是大于零的常数.  时,求
时,求 的极值;
的极值; 上为单调递增,求实数
上为单调递增,求实数 上存在一点
上存在一点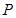 ,使得曲线
,使得曲线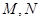 ,且
,且 成立.
成立.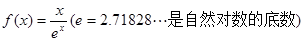 .
.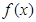 的单调区间及最大值;
的单调区间及最大值;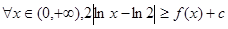 恒成立,试求实数
恒成立,试求实数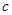 的取值范围.
的取值范围. .
. 在
在 处取得极大值,求实数
处取得极大值,求实数 的值;
的值; ,求
,求 上的最大值.
上的最大值.