题目内容
(本题满分16分)
已知抛物线C的顶点在坐标原点,准线l的方程为x=-2,点P在准线上l上,纵坐标为![]() ,点Q在y轴上,纵坐标为2t。
,点Q在y轴上,纵坐标为2t。
求抛物线C的方程;
求证:直线PQ恒与一个圆心在x轴是的定圆M相切,并求圆M的方程。
(1)设抛物线![]() 的方程为
的方程为![]() ,
,
因为准线![]() 的方程为
的方程为![]() ,所以
,所以![]() ,即
,即![]() ,
,
因此抛物线![]() 的方程为
的方程为![]() . …………………………………………………………4分
. …………………………………………………………4分
(2)由题意可知,![]() ,
,![]() ,
,
则直线![]() 方程为:
方程为: ,即
,即![]() ,………………8分
,………………8分
设圆心在![]() 轴上,且与直线
轴上,且与直线![]() 相切的圆
相切的圆![]() 的方程为
的方程为![]() ,
,
则圆心![]() 到直线
到直线![]() 的距离
的距离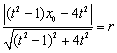 , …………………………………10分
, …………………………………10分
即![]() ①,或
①,或![]() ② ,
② ,
由①可得![]() 对任意
对任意![]() 恒成立,则有
恒成立,则有
![]() ,解得
,解得![]() (舍去),……………………………………………………14分
(舍去),……………………………………………………14分
由②可得![]() 对任意
对任意![]() 恒成立,则有
恒成立,则有
![]() ,可解得
,可解得![]()
因此直线![]() 恒与一个圆心在
恒与一个圆心在![]() 轴上的定圆
轴上的定圆![]() 相切,圆
相切,圆![]() 的方程为
的方程为![]() .
.
…………………………………………………………………………………………………16分

练习册系列答案
相关题目


 在
在 上的单调性;
上的单调性; ,使
,使 ,则称
,则称 的不动点,现已知该函数有且仅有一个不动点,求
的不动点,现已知该函数有且仅有一个不动点,求 的值;
的值; 在
在