Question

有一种大型商品,A、B两地都有出售,且价格相同.某地居民从两地之一购得商品后,回运的费用是:每单位距离A地的运费是B地运费的3倍,已知A、B两地距离10 km,顾客选A地或B地购买这件商品的标准是:包括运费和价格的总费用较低,求A、B两地的售货区域的分界线的曲线形状,并指出曲线上、曲线内、曲线外的居民应如何选择购货地点.

Answer 1

思路分析:首先要建立以A或B为中心的购买区域,因为每单位距离A地的运费是B地运费的3倍,因此,顾客所在地到A地距离是到B地距离的,以此为等量关系,所以满足此条件的范围应为某区域,我们可以建立以AB为横轴的直角坐标系.

解:以A、B所确定的直线为x轴,A、B中点O为坐标原点,建立直角坐标系.如图4-1-4,则A(-5,0)、B(5,0).

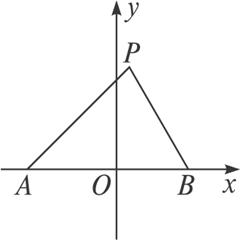
图4-1-4

设某地P的坐标为(x,y),且P地居民选择A地购买商品便宜,并设A地的运费为3a 元/km,B地的运费为a 元/km.

价格+x_A地运费≤价格+x_B地运费,

所以3a

因为a＞0,所以3.

两边平方,得9(x+5)²+9y²≤(x-5)²+y²,即(x+)²+y²≤()².

所以,以点C(,0)为圆心、为半径的圆是这两地购货的分界线.

圆C内的居民从A地购货便宜;圆C外的居民从B地购货便宜;

圆C上的居民从A、B两地购货的总费用相等,因此,可随意从A、B两地之一购货.

  绿色通道:(1)坐标法是研究解析几何问题的一个重要方法,在解决实际问题时要注意建立适当的直角坐标系,用坐标法进行求解.

(2)在学习中要注意联系实际,重视数学在生产、生活及相关学科中的运用.

(3)解有关实际应用题时,关键要明确题意,掌握建立数学模型的基本方法.