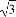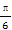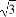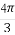Question

已知:0°<α<90°,0°<α+β<90°,3sinβ=sin(2α+β),则tanβ的最大值是　　　　.

 

Answer 1

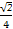
【解析】由3sinβ=sin(2α+β)得3sin(α+β-α)=sin(α+β+α),化简得sin(α+β)cosα=2cos(α+β)sinα,

∴tan(α+β)=2tanα,

∴tanβ=tan(α+β-α)=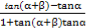

==.

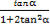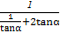由题意知,tanα>0,

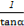∴+2tanα≥2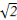

(当且仅当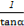=2tanα,即tanα=时等号成立),

∴tanβ的最大值为=.

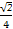【方法技巧】三角函数和差公式的灵活应用

(1)三角函数和差公式在三角函数式的化简和求值中经常用到,因此公式的灵活应用非常关键,公式可以正用、逆用、变形应用.

(2)逆用关键在于构造公式的形式,方法是通过三角恒等变换,出现和或差的形式,即出现能逆用公式的条件;有时通过两式平方相加减,利用平方关系式,切函数化成弦函数等技巧.